I. Les transitions par bandes▲
Les programmes de test sont présents dans le répertoire exemples accompagnant le tutoriel.
Certaines transitions répètent un motif sur la zone d'affichage. Afin d'illustrer ce cas, nous allons construire une série de transitions qui dessineront des rectangles régulièrement espacés pour faire apparaître l'image de destination. L'espacement sera vertical ou horizontal.
I-A. Les bandes horizontales▲
[Exemple BGRABitmap 22]
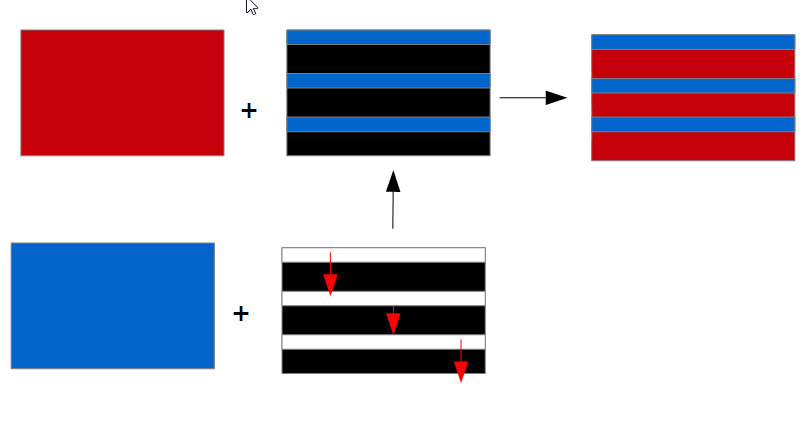
Il s'agit dans un premier temps de produire des bandes horizontales. Le principe est de diviser la hauteur de l'image par le nombre de bandes et de commencer à dessiner l'image de destination depuis les points ainsi trouvés. Chaque bande (rectangle) commencera à un point et ira jusqu'au point suivant (vers le haut ou vers le bas) en suivant le rythme des étapes, donc de 0 à 100 pour notre application de démonstration.
La transition StripsDown nous servira de modèle.
Son schéma de fonctionnement avec un calque sera celui-ci :
Pour nos essais, nous déclarerons une constante C_NumberOfStrips qui fournira le nombre de bandes à dessiner. Comme pour les points de la spline, nous envisagerons ultérieurement le choix de ce nombre par l'utilisateur lui-même.
Grâce à cette constante, nous pourrons calculer aisément l'ordonnée de départ de chacune des bandes. Les abscisses sont par ailleurs déjà connues puisque les bandes occuperont en permanence toute la largeur de l'image.
Comme la hauteur de l'image est quelconque, nous pourrions nous heurter à deux problèmes. Le premier proviendrait du fait que la hauteur ne serait pas exactement divisible par le nombre de bandes si bien qu'il nous faudrait en tenir compte afin de bien recouvrir toute la surface de l'image : pour éviter ce problème potentiel, nous prévoirons systématiquement une bande supplémentaire. Bien que peu probable, le second problème surgirait si la hauteur était plus petite en pixels que le nombre de bandes : ce cas ne sera pas traité pour le moment, mais nous devrons le garder en tête pour le composant final.
Pour rendre les calculs plus clairs, nous définirons aussi une variable locale LStripHeight qui contiendra la hauteur de la bande en fonction du nombre de bandes et de la hauteur de l'image.
Voici le code proposé :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
const
C_NumberOfStrips = 10;
var
LBGRAFrom, LBGRATo, LBGRAMask: TBGRABitmap;
LY, LX, LI, LStripHeight: Integer;
begin
btnGo.Enabled := False;
// calcul de la hauteur d'une bande + 1 pour les arrondis
LStripHeight := 1 + imgResult.ClientHeight div C_NumberOfStrips;
LBGRAFrom := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRATo := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRAMask := TBGRABitmap.Create(imgResult.ClientWidth, ClientHeight, BGRABlack);
try
fStep := 0;
repeat
Inc(fStep);
LX := 0;
LY := 0;
LBGRAFrom.Fill(BGRABlack);
LBGRAFrom.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
// nous traçons les bandes
for LI := 0 to C_NumberOfStrips - 1 do
begin
// chaque bande est un rectangle
LBGRAMask.FillRectAntialias(0, LStripHeight * LI,
imgResult.ClientWidth,
LStripHeight * fStep div 100 + LStripHeight * LI,
BGRAWhite);
end;
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRAMask.Free;
end;
finally
LBGRATo.Free;
end;
finally
LBGRAFrom.Free;
btnGo.Enabled := True;
end;
end;Le code ressemble beaucoup à ce qui a déjà été étudié. Une copie instantanée d'écran a donné :
La réciproque de cette transition sera appelée StripsUp. Sans surprise, le cœur du code nécessaire sera :
for LI := 1 to C_NumberOfStrips do
begin
LBGRAMask.FillRectAntialias(0, LStripHeight * LI - LStripHeight * fStep div 100,
imgResult.ClientWidth,
LStripHeight * LI,
BGRAWhite);
end;I-B. Les bandes verticales▲
[Exemple BGRABitmap 23]
La réalisation de bandes verticales est très proche de celle de bandes horizontales si bien que nous allons en profiter pour introduire une autre façon que l'emploi d'une constante pour gérer le nombre de bandes.
Nous allons donc créer une fonction nommée NumberOfStrips imbriquée dans le gestionnaire OnClick dont nous nous servons sans cesse. Cette fonction retournera le nombre de bandes selon la largeur de l'image à produire : 1 bande pour une image de moins de 10 pixels de largeur ; 5 bandes pour moins de 300 pixels ; la largeur divisée par C_DefaultNumberOfStrips (une constante fixée à 20) pour moins de 1000 pixels ; 30 bandes pour les images plus larges.
Les valeurs choisies ont été fixées empiriquement. Le nombre de bandes par défaut bénéficie d'une constante, car il s'agit d'une valeur susceptible d'être modifiée selon les goûts de chacun !
Après avoir été toutes nommées, ces constantes pourront être regroupées dans une unité à part.
Voici le code proposé :
function NumberOfStrips: Integer;
const
C_DefaultNumberOfStrips = 20;
begin
if imgResult.ClientWidth < 10 then
Result := 1
else
if (imgResult.ClientWidth < 300) then
Result := 5
else
if (imgResult.ClientWidth < 1000) then
Result := imgResult.ClientWidth div C_DefaultNumberOfStrips
else
Result := 30;
end;Il sera bien entendu avantageux de proposer par la suite une fonction plus générale qui prendra aussi en compte la hauteur de l'image : il suffira pour cela d'introduire un paramètre qui remplacera la donnée figée ClientWidth. Mieux encore, le composant final autorisera le choix entre un calcul automatique du nombre de bandes et une entrée manuelle des valeurs.
Pour ce qui est du code de la transition StripsLeft, voici que nous pouvons écrire :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
var
LBGRAFrom, LBGRATo, LBGRAMask: TBGRABitmap;
LY, LX, LI, LStripWidth: Integer;
function NumberOfStrips: Integer;
const
C_DefaultNumberOfStrips = 20;
begin
if imgResult.ClientWidth < 10 then
Result := 1
else
if (imgResult.ClientWidth < 300) then
Result := 5
else
if (imgResult.ClientWidth < 1000) then
Result := imgResult.ClientWidth div C_DefaultNumberOfStrips
else
Result := 30;
end;
begin
btnGo.Enabled := False;
LStripWidth := 1 + imgResult.ClientWidth div NumberOfStrips;
LBGRAFrom := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRATo := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRAMask := TBGRABitmap.Create(imgResult.ClientWidth, ClientHeight, BGRABlack);
try
fStep := 0;
repeat
Inc(fStep);
LX := 0;
LY := 0;
LBGRAFrom.Fill(BGRABlack);
LBGRAFrom.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
for LI := 0 to NumberOfStrips do
begin
LBGRAMask.FillRectAntialias(LStripWidth * LI - LStripWidth * fStep div 100, 0,
LStripWidth * LI,
imgResult.ClientHeight, BGRAWhite);
end;
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRAMask.Free;
end;
finally
LBGRATo.Free;
end;
finally
LBGRAFrom.Free;
btnGo.Enabled := True;
end;
end;Ce sont à présent les ordonnées qui sont constantes en recouvrant toute la hauteur de l'image. Partant d'une position fixe déterminée par LI, les rectangles s'agrandissent vers la gauche de l'image en fonction de l'étape à réaliser.
Un instantané de cette transition donnera par exemple :
En diminuant fortement la largeur de l'image finale jusqu'à ce qu'elle ait une valeur inférieure à 300 pixels, nous obtiendrons par exemple, sans calculs supplémentaires :
Nous pouvons de la même manière créer la transition StripsRight. Nous n'en proposerons que le code et une vidéo de démonstration :
for LI := 0 to NumberOfStrips - 1 do
begin
// chaque bande est un rectangle
LBGRAMask.FillRectAntialias(LStripWidth * LI, 0,
LStripWidth * fStep div 100 + LStripWidth * LI,
imgResult.ClientHeight, BGRAWhite);
end;I-C. Entrelacer les bandes▲
[Exemple BGRABitmap 24]
Entrelacer des bandes repose sur le même principe que leur dessin horizontalement ou verticalement, à savoir l'agrandissement progressif de rectangles selon une seule dimension. La différence essentielle tient au fait qu'un rectangle suivant un autre croîtra à partir du bord opposé de l'image. Un schéma représentant le masque de ce mécanisme si l'entrelacement est horizontal pourra être celui-ci :
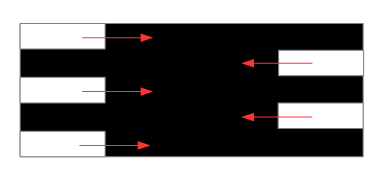
Tout de suite apparaît un problème spécifique à ce type de transition : commencerons-nous par la bande qui se déplace vers la droite ou au contraire par celle qui se dirige vers la gauche ? Pour le dessin, nous utiliserons comme ci-avant une itération, ainsi pourrons-nous décider du dessin à partir de la parité du numéro de la bande. Nous baptiserons StripsInterlacedLeftRight la première transition et StripsInterlacedRightLeft la seconde.
Le code proposé pour StripsInterlacedLeftRight tient compte de la difficulté évoquée en utilisant la fonction Odd :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
var
LBGRAFrom, LBGRATo, LBGRAMask: TBGRABitmap;
LY, LX, LI, LStripHeight: Integer;
function NumberOfStrips: Integer;
const
C_DefaultNumberOfStrips = 20;
begin
if imgResult.ClientHeight < 10 then
Result := 1
else
if (imgResult.ClientHeight < 300) then
Result := 5
else
if (imgResult.ClientHeight < 1000) then
Result := imgResult.ClientHeight div C_DefaultNumberOfStrips
else
Result := 30;
end;
begin
btnGo.Enabled := False;
LStripHeight := 1 + imgResult.ClientHeight div NumberOfStrips;
LBGRAFrom := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRATo := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRAMask := TBGRABitmap.Create(imgResult.ClientWidth, ClientHeight, BGRABlack);
try
fStep := 0;
repeat
Inc(fStep);
LX := 0;
LY := 0;
LBGRAFrom.Fill(BGRABlack);
LBGRAFrom.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
for LI := 0 to NumberOfStrips do
if Odd(LI) then
LBGRAMask.FillRectAntialias(imgResult.ClientWidth
- imgResult.ClientWidth * fStep div 100, LStripHeight * LI,
imgResult.ClientWidth,
LStripHeight * (LI + 1), BGRAWhite, False)
else
LBGRAMask.FillRectAntialias(0, LStripHeight * LI,
imgResult.ClientWidth * fStep div 100,
LStripHeight * (LI + 1), BGRAWhite, False);
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRAMask.Free;
end;
finally
LBGRATo.Free;
end;
finally
LBGRAFrom.Free;
btnGo.Enabled := True;
end;
end;Pour passer de StripsInterlacedLeftRight à StripsInterlacedRightLeft, il nous faudra tout simplement inverser le résultat de la fonction Odd :
for LI := 0 to NumberOfStrips - 1 do
if not Odd(LI) then // ici, l'unique modificationUne capture d'écran correspondant à StripsInterlacedLeftRight a donné :
Le travail similaire à effectuer pour des bandes verticales ne devrait pas poser de problèmes. Bien sûr, il faudra nous souvenir d'utiliser la largeur de l'image pour le calcul automatique des bandes. Voici le code nécessaire à la transition que nous nommerons StripsInterlacedDownUp :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
var
LBGRAFrom, LBGRATo, LBGRAMask: TBGRABitmap;
LY, LX, LI, LStripWidth: Integer;
function NumberOfStrips: Integer;
const
C_DefaultNumberOfStrips = 20;
begin
if imgResult.ClientWidth < 10 then
Result := 1
else
if (imgResult.ClientWidth < 300) then
Result := 5
else
if (imgResult.ClientWidth < 1000) then
Result := imgResult.ClientWidth div C_DefaultNumberOfStrips
else
Result := 30;
end;
begin
btnGo.Enabled := False;
LStripWidth := 1 + imgResult.ClientWidth div NumberOfStrips;
LBGRAFrom := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRATo := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRAMask := TBGRABitmap.Create(imgResult.ClientWidth, ClientHeight, BGRABlack);
try
fStep := 0;
repeat
Inc(fStep);
LX := 0;
LY := 0;
LBGRAFrom.Fill(BGRABlack);
LBGRAFrom.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
for LI := 0 to NumberOfStrips do
if Odd(LI) then
LBGRAMask.FillRectAntialias(LStripWidth * LI,
0, LStripWidth * (LI + 1),
imgResult.ClientHeight * fStep div 100,
BGRAWhite, False)
else
LBGRAMask.FillRectAntialias(LStripWidth * LI,
imgResult.ClientHeight - imgResult.ClientHeight * fStep div 100,
LStripWidth * (LI + 1),
imgResult.ClientHeight,
BGRAWhite, False);
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRAMask.Free;
end;
finally
LBGRATo.Free;
end;
finally
LBGRAFrom.Free;
btnGo.Enabled := True;
end;
end;Nous savons que, comme précédemment, sa sœur StripsInterlacedUpDown ne nécessitera qu'une inversion du résultat de la fonction Odd :
for LI := 0 to NumberOfStrips do
if not Odd(LI) then // unique modificationVoici une capture d'écran de StripsInterlacedDownUp à mi-parcours de son action :
I-D. Combinaisons de bandes▲
[Exemple BGRABitmap 25]
Une variante du travail précédent consisterait à travailler simultanément avec les bandes horizontales et verticales. Par exemple, nous pouvons décider de dessiner des rectangles qui se formeraient alternativement en recouvrant vers le bas puis vers le haut l'image d'origine. Le principe de cette transition est fourni par la portion de schéma suivante :
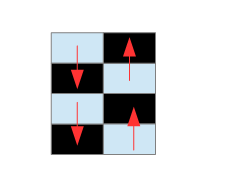
Ce schéma décrit une transition que nous pourrions baptiser RectDownUp puisqu'elle commence par un recouvrement en descendant. Son pendant serait alors RectUpDown qui commencerait par un rectangle dessiné en remontant.
Le code correspondant de RectUpDown serait :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
var
LBGRAFrom, LBGRATo, LBGRAMask: TBGRABitmap;
LY, LX, LI, LJ, LStripHeight, LStripWidth, LNumHeight, LNumWidth: Integer;
function NumberOfStrips(AValue: Integer): Integer;
const
C_DefaultNumberOfStrips = 20;
begin
if AValue < 10 then
Result := 1
else
if AValue < 300 then
Result := 5
else
if AValue < 1000 then
Result := AValue div C_DefaultNumberOfStrips
else
Result := 30;
end;
begin
btnGo.Enabled := False;
LNumHeight:= NumberOfStrips(imgResult.ClientHeight);
LNumWidth:= NumberOfStrips(imgResult.ClientWidth);
LStripHeight := 1 + imgResult.ClientHeight div LNumHeight;
LStripWidth := 1 + imgResult.ClientWidth div LNumWidth;
LBGRAFrom := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRATo := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRAMask := TBGRABitmap.Create(imgResult.ClientWidth, ClientHeight, BGRABlack);
try
fStep := 0;
repeat
Inc(fStep);
LX := 0;
LY := 0;
LBGRAFrom.Fill(BGRABlack);
LBGRAFrom.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
for LI := -1 to LNumWidth do
if Odd(LI) then
for LJ := -1 to LNumHeight do
if Odd(LJ) then
LBGRAMask.FillRectAntialias(LStripWidth * LI,
LStripHeight * LJ,
LStripWidth * (LI + 1),
LStripHeight * LJ + 2 * LStripHeight * fStep div 100,
BGRAWhite, False)
else
LBGRAMask.FillRectAntialias(LStripWidth * (LI + 1),
LStripHeight * (LJ + 1) - 2 * LStripHeight * fStep div 100,
LStripWidth * (LI + 2),
LStripHeight * (LJ +1),
BGRAWhite, False);
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRAMask.Free;
end;
finally
LBGRATo.Free;
end;
finally
LBGRAFrom.Free;
btnGo.Enabled := True;
end;
end;Il nous faudra prendre garde à la hauteur des rectangles tels qu'ils ont été définis afin de les recouvrir entièrement. Nous obtenons alors des images comme celle qui suit :
Comme annoncé au début de son introduction, la fonction NumberOfStrips a dû être assouplie afin d'accepter aussi bien une largeur qu'une hauteur.
Nous aurons deviné que la sœur de RectUpDown , c'est-à -dire RectDownUp, s'obtiendra en modifiant par une négation le retour de la fonction Odd :
for LI := -1 to LNumWidth do
if not Odd(LI) then // seule modification
for LJ := -1 to LNumHeight do
if Odd(LJ) thenII. L'utilisation des splines▲
II-A. Limites des outils actuels▲
Cette fois-ci, nous pouvons considérer que nous avons épuisé le filon des transitions à base de rectangles. Enfin, presque : nous verrons qu'ils entreront de nouveau en scène avec les rotations et les homothéties !
Nous aurions aussi pu exploiter la méthode RoundRectAntialias dont les différentes déclinaisons autorisent le dessin de rectangles aux sommets arrondis.
En voici les définitions au sein de la classe TBGRABitmap :
{** Fills a rounded rectangle with antialiasing. The corners have an
elliptical radius of ''rx'' and ''ry''. ''options'' specifies how to
draw the corners. See [[BGRABitmap Geometry types|geometry types]] }
procedure FillRoundRectAntialias(x,y,x2,y2,rx,ry: single; c: TBGRAPixel; options: TRoundRectangleOptions = []; pixelCenteredCoordinates: boolean = true); override;
{** Fills a rounded rectangle with a texture }
procedure FillRoundRectAntialias(x,y,x2,y2,rx,ry: single; texture: IBGRAScanner; options: TRoundRectangleOptions = []; pixelCenteredCoordinates: boolean = true); override;Comme l'expliquent les commentaires joints aux déclarations, il s'agit avant tout de définir un rectangle aux coins arrondis grâce à deux rayons ellipsoïdaux et des options qui indiquent la forme de l'arrondi pour chacun des sommets. Nous n'analyserons pas plus ces méthodes qui présentent un intérêt restreint pour le sujet des transitions.
Avec les méthodes employées jusqu'à présent pour dessiner, nous avons presque uniquement eu affaire à des polygones, donc à des angles vifs. Tout au plus avons-nous croisé des ellipses facilement transformables en cercles. Nous voici donc limités à des formes géométriques de base avec lesquelles nous pouvons faire beaucoup, mais souvent avec des calculs ardus dès qu'il s'agit d'obtenir des courbes douces. Et si nous tentions de sortir de ce carcan ?
II-B. Les splines▲
Ce sont les splines qui vont lever ces limitations en proposant des courbes adoucies très appréciables par exemple lorsque nous chercherons à imiter un liquide. Selon Wikipédia, « en mathématiques appliquées et en analyse numérique, une spline est une fonction définie par morceaux par des polynômes ». L'article précise qu'elles sont très utilisées dans les problèmes d'interpolation et dans ceux liés au lissage de données expérimentales ou de statistiques.
Le plus simple pour comprendre leur intérêt est de produire une transition avec les outils actuellement en notre possession et d'appliquer ensuite ce nouvel outil. Nous allons proposer une animation qui fera « couler » l'image de destination depuis le sommet de l'image d'origine. Les coulures seront aléatoires afin d'améliorer le mimétisme de la transition.
Voici le schéma avec calque qui lui est associé :
II-B-1. Première Ă©tape sans spline▲
[Exemple BGRABitmap 26]
Dans un premier temps, nous nous contenterons d'utiliser les polygones pour une approximation de cet objectif. Nous allons par conséquent créer un tableau de points qui contiendra ceux du polygone d'origine : nous voulons que les points supérieur gauche et supérieur droit ne bougent pas afin de toujours garder le bord supérieur de l'image comme frontière supérieure, mais que les autres points aient leur ordonnée tirée au hasard puis graduellement augmentée jusqu'à toucher le bord inférieur de l'image à la centième étape.
Du point de vue du code, nous aurons donc quelque chose comme :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
const
C_Points = 20;
var
LBGRAFrom, LBGRATo, LBGRAMask: TBGRABitmap;
LY, LX, LI: Integer;
LPts, LPtsTemp: array of TPointF;
begin
btnGo.Enabled := False;
LBGRAFrom := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRATo := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRAMask := TBGRABitmap.Create(imgResult.ClientWidth, ClientHeight, BGRABlack);
try
fStep := 0;
// préparation des tableaux
SetLength(LPts, C_Points);
SetLength(LPtsTemp, C_Points);
// remplissage du tableau temporaire de travail
// et de spoints extrĂŞmes qui ne changeront pas
LPts[0] := PointF(0, 0);
LPtsTemp[1] := PointF(0, 0);
LPts[Length(LPts) - 1] := PointF(imgResult.ClientWidth, 0);
LPtsTemp[Length(LPts) - 2] := PointF(imgResult.ClientWidth, 0);
for LI := 2 to Length(LPts) - 3 do
begin
LPtsTemp[LI].x := imgResult.ClientWidth / Length(LPts) * LI;
// une astuce qui permet d'accentuer les coulures
if random < 0.6 then
// l'ordonnée est tirée au hasard
LPtsTemp[LI].y := random(imgResult.ClientHeight div 3)
else
// ou vaut 0
LPtsTemp[Li].y := 0;
end;
repeat
Inc(fStep);
// traitement 1 ici (source)
LX := 0;
LY := 0;
LBGRAFrom.Fill(BGRABlack);
LBGRAFrom.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
// traitement 2 ici (destination)...
LBGRAMask.Fill(BGRABlack);
// les ordonnées augmentent selon la position d'origine
// l'Ă©tape en cours
for LI := 1 to Length(LPts) - 2 do
begin
LPts[LI].x := LPtsTemp[LI].x;
LPts[LI].y := LPtsTemp[LI].y + (imgResult.ClientHeight - LPtsTemp[LI].y) * fStep / 100;
end;
// le polygone est dessiné et rempli
LBGRAMask.FillPolyAntialias(LPts, BGRAWhite);
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRAMask.Free;
end;
finally
LBGRATo.Free;
end;
finally
LBGRAFrom.Free;
btnGo.Enabled := True;
end;
end;Le code est suffisamment commenté pour en comprendre les principales étapes. Une difficulté tient aux extrémités qui doivent apparemment à la fois rester immobiles et se déplacer vers le bas : en fait, il s'agit d'un polygone dont des sommets sont confondus au début de la transition. La solution est de les représenter avec des points aux destins différents.
Une amélioration à apporter à ce code consisterait à faire disparaître la constante numérique C_Points utilisée pour le nombre de points de la courbe. Elle serait alors remplacée, soit par un calcul en fonction de la largeur de l'image, soit par un paramètre fourni par l'utilisateur. Vous aurez cependant sans doute remarqué que cette constante n'a été utilisée que pour l'initialisation des tableaux, les formules de calculs lui préférant la fonction Length appliquée à la structure.
Pour le moment, le résultat n'est pas tout à fait celui escompté :
Les angles des coulures sont bien trop saillants par endroits ! La question qui se pose est alors : comment pourrions-nous lisser cette courbe pour en faire disparaître les angles vifs ?
II-B-2. Seconde Ă©tape avec spline▲
[Exemple BGRABitmap 27]
Nous connaissons la solution de ce problème puisque les splines répondent par définition à ce type de question.
Pour mettre en œuvre les splines, nous allons déclarer un tableau ouvert de TPointF que nous appellerons LSpline et grâce auquel nous calculerons la nouvelle courbe. De plus, nous remplacerons la ligne de dessin avec FillPolyAntialias par les deux lignes suivantes :
LSpline := LBGRAMask.ComputeOpenedSpline(LPts, ssOutside);
LBGRAMask.DrawPolyLineAntialias(LSpline, BGRAWhite, 1, BGRAWhite);La première ligne calcule grâce à la méthode ComputeOpenedSpline les nouveaux points et les affecte à notre nouvelle variable tandis que la seconde dessine la courbe obtenue précédemment grâce à la méthode DrawPolylineAntialias.
Cette fois-ci, voici ce que nous obtenons :
C'est exactement ce que nous cherchions à faire !
La routine complète de dessin est alors :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
const
C_Points = 20;
var
LBGRAFrom, LBGRATo, LBGRAMask: TBGRABitmap;
LY, LX, LI: Integer;
LPts, LPtsTemp, LSpline: array of TPointF;
begin
btnGo.Enabled := False;
LBGRAFrom := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRATo := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRAMask := TBGRABitmap.Create(imgResult.ClientWidth, ClientHeight, BGRABlack);
try
fStep := 0;
SetLength(LPts, C_Points);
SetLength(LPtsTemp, C_Points);
LPts[0] := PointF(0, 0);
LPtsTemp[1] := PointF(0, 0);
LPts[Length(LPts) - 1] := PointF(imgResult.ClientWidth, 0);
LPtsTemp[Length(LPts) - 2] := PointF(imgResult.ClientWidth, 0);
for LI := 2 to Length(LPts) - 3 do
begin
LPtsTemp[LI].x := imgResult.ClientWidth / Length(LPts) * LI;
if random < 0.6 then
LPtsTemp[LI].y := random(imgResult.ClientHeight div 3)
else
LPtsTemp[Li].y := 0;
end;
repeat
Inc(fStep);
// traitement 1 ici (source)
LX := 0;
LY := 0;
LBGRAFrom.Fill(BGRABlack);
LBGRAFrom.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
// traitement 2 ici (destination)...
LBGRAMask.Fill(BGRABlack);
for LI := 1 to Length(LPts) - 2 do
begin
LPts[LI].x := LPtsTemp[LI].x;
LPts[LI].y := LPtsTemp[LI].y + (imgResult.ClientHeight - LPtsTemp[LI].y) * fStep / 100;
end;
LSpline := LBGRAMask.ComputeOpenedSpline(LPts, ssOutside);
LBGRAMask.DrawPolyLineAntialias(LSpline, BGRAWhite, 1, BGRAWhite);
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRAMask.Free;
end;
finally
LBGRATo.Free;
end;
finally
LBGRAFrom.Free;
btnGo.Enabled := True;
end;
end;Comme cette transition est assez originale et esthétique, voici un petit film qui la montre en action :
II-C. Examen des nouvelles mĂ©thodes▲
Les nouvelles méthodes introduites méritent que nous nous y arrêtions un instant. La première est ComputeOpenedSpline qui, comme son nom l'indique, calcule une spline pour une courbe ouverte.
Sa déclaration se présente ainsi :
function ComputeOpenedSpline(const APoints: array of TPointF; AStyle: TSplineStyle): ArrayOfTPointF; override;Nous voyons qu'elle prend pour paramètres un tableau de points (de type TPointF avec des coordonnées flottantes) et un style de type TSplineStyle. Ce dernier permet de construire la courbe selon l'effet recherché en fonction de l'enveloppe du polygone de départ, c'est-à -dire le polygone obtenu en suivant le contour extérieur du polygone de référence :
|
Style |
Effet |
|
ssInside |
La courbe est dessinée à l'intérieur de l'enveloppe du polygone sans inclure les points de début et de fin |
|
ssInsideWithEnds |
Idem mais en incluant les points de début et de fin |
|
ssCrossing |
La courbe traverse l'enveloppe du polygone sans inclure les points de début et de fin |
|
ssCrossingWithEnds |
Idem mais en incluant les points de début et de fin |
|
ssOutside |
La courbe est dessinée à l'extérieur de l'enveloppe du polygone en incluant les points de début et de fin |
|
ssRoundOutside |
La courbe s'étend à l'extérieur de l'enveloppe du polygone en incluant les points de début et de fin |
|
ssVertexToSide |
La courbe est située à l'extérieur de l'enveloppe du polygone et est calculée à partir des tangentes aux points choisis en incluant les points de début et de fin |
Certains des styles ne permettent pas d'obtenir un recouvrement complet de l'image d'origine. Par exemple, avec nos formules et les coordonnées choisies, les quatre premiers styles du tableau ne conviennent pas.
Un peu plus loin, dans le prochain exemple, nous verrons en action les différences entre ces options.
La valeur retournée par la fonction est un tableau qui contient les points de la courbe arrondie : c'est ce tableau qui sera finalement dessiné.
ComputeOpenedSpline a pour pendant la méthode ComputeClosedSpline qui ferme la spline. Dans l'exemple choisi, la différence n'était pas perceptible puisque nous nous appuyions sur le bord supérieur de l'image pour former une frontière à la surface de la courbe.
La seconde méthode nouvelle est DrawPolyLineAntialias. Comme son nom l'indique, elle dessine avec anticrénelage une ligne continue composée d'un ou de plusieurs segments de ligne. Comme aussi bon nombre des méthodes présentées, elle a de multiples variétés grâce à la surcharge des déclarations :
{** Draws a polyline using current pen style/cap/join }
procedure DrawPolyLineAntialias(const points: array of TPointF; c: TBGRAPixel; w: single); override;
{** Draws a polyline using current pen style/cap/join.
''texture'' specifies the source color to use when filling the line }
procedure DrawPolyLineAntialias(const points: array of TPointF; texture: IBGRAScanner; w: single); override;
{** Draws a polyline using current pen style/cap/join.
''Closed'' specifies if the end of the line is closed. If it is not closed,
a space is left so that the next line can fit }
procedure DrawPolyLineAntialias(const points: array of TPointF; c: TBGRAPixel; w: single; ClosedCap: boolean); override;
procedure DrawPolyLineAntialias(const points: array of TPointF; texture: IBGRAScanner; w: single; ClosedCap: boolean); override;
{** Draws a polyline using current pen style/cap/join.
''fillcolor'' specifies a color to fill the polygon formed by the points }
procedure DrawPolyLineAntialias(const points: array of TPointF; c: TBGRAPixel; w: single; fillcolor: TBGRAPixel); override;Nous voyons que nous pouvons jouer sur les points, les couleurs, les textures, les jointures, la couleur de remplissage, l'épaisseur du trait (paramètre w) ou l'apparence de la fin de la ligne pour un éventuel raccord. Pour le masque, nous avons choisi la dernière mouture de la méthode puisque nous désirions peindre en blanc la surface délimitée par la courbe calculée.
Ces procédures mériteraient à elles seules un développement particulier qui nous conduirait bien loin de notre préoccupation première !
II-D. Application Ă©tendue des splines▲
Les transitions décrites jusqu'à présent reposaient la plupart du temps sur l'utilisation d'un ou de plusieurs polygones (triangles et rectangles pour l'essentiel). En appliquant l'outil de la spline à ces transitions, nous pouvons espérer obtenir des animations proches de l'original, mais aux formes adoucies.
[Exemple BGRABitmap 28]
Reprenons par exemple la transition RightBottomExpand qui agrandit un rectangle en direction du point inférieur droit de l'image finale, recouvrant peu à peu l'image d'origine par celle de destination. Nous pouvons stocker dans un tableau les coordonnées du rectangle qui sert au dessin, calculer une spline à partir d'elles, avant de dessiner le résultat sur notre masque.
Le code donnera alors ceci :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
var
LBGRAFrom, LBGRATo, LBGRAMask: TBGRABitmap;
LY, LX: Integer;
LPts, LSpline: array of TPointF;
begin
btnGo.Enabled := False;
LBGRAFrom := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRATo := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
LBGRAMask := TBGRABitmap.Create(imgResult.ClientWidth, ClientHeight, BGRABlack);
try
fStep := 0;
repeat
Inc(fStep);
LX := 0;
LY := 0;
LBGRAFrom.Fill(BGRABlack);
LBGRAFrom.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
SetLength(LPts, 4);
LBGRAMask.Fill(BGRABlack);
//LBGRAMask.FillRectAntialias(0, 0, imgResult.ClientWidth * fStep div 100,
// imgResult.ClientHeight * fStep div 100, BGRAWhite);
LPts[0] := PointF(0, 0);
LPts[1] := PointF(imgResult.ClientWidth * fStep div 100, 0);
LPts[2] := PointF(imgResult.ClientWidth * fStep div 100, imgResult.ClientHeight * fStep div 100);
LPts[3] := PointF(0, imgResult.ClientHeight * fStep div 100);
LSpline := LBGRAMask.ComputeClosedSpline(LPts, ssVertexToSide);
LBGRAMask.DrawPolyLineAntialias(LSpline, BGRAWhite, 1, BGRAWhite);
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRAMask.Free;
end;
finally
LBGRATo.Free;
end;
finally
LBGRAFrom.Free;
btnGo.Enabled := True;
end;
end;Les deux lignes de calculs mises en commentaire sont les deux lignes originales Ă©crites pour la transition sans spline.
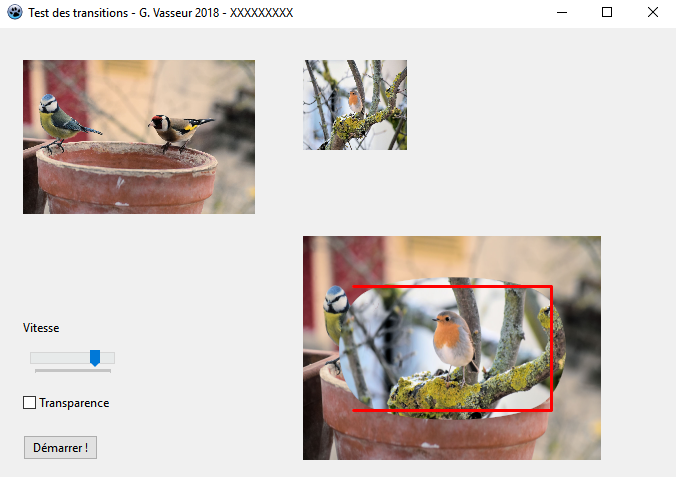
La transition dessine désormais une forme arrondie proche de l'ellipse :

Afin de visualiser les différences entre les options associées au calcul de la spline, nous ajouterons une ligne provisoire à notre code :
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);
LBGRAFrom.DrawPolylineAntialias(LPts,BGRA(255,0,0,255),3); // nouvelle ligne
LBGRAFrom.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;Nous allons aussi décaler le dessin de 50 pixels afin de mieux visualiser les différences de tracé suivant l'option active :
SetLength(LPts, 4);
LBGRAMask.Fill(BGRABlack);
//LBGRAMask.FillRectAntialias(0, 0, imgResult.ClientWidth * fStep div 100,
// imgResult.ClientHeight * fStep div 100, BGRAWhite);
LPts[0] := PointF(50, 50);
LPts[1] := PointF(50 + (imgResult.ClientWidth - 100) * fStep div 100, 50);
LPts[2] := PointF(50 + (imgResult.ClientWidth - 100) * fStep div 100, 50 + (imgResult.ClientHeight - 100) * fStep div 100);
LPts[3] := PointF(50, 50 + (imgResult.ClientHeight - 100) * fStep div 100);
LSpline := LBGRAMask.ComputeClosedSpline(LPts, ssVertexToSide);
LBGRAMask.DrawPolyLineAntialias(LSpline, BGRAWhite, 1, BGRAWhite);
LBGRATo.PutImage(0, 0, fBGRATo, dmSet);
LBGRATo.ApplyMask(LBGRAMask);
LBGRAFrom.PutImage(0, 0, LBGRATo, dmDrawWithTransparency, Opacity);La forme d'origine de la ligne multiple est reproduite au fur et à mesure de la transition. Elle est d'autant plus visible que sa couleur de dessin est le rouge. Il ne nous reste qu'à modifier le dernier paramètre de la méthode ComputeClosedSpline pour voir les résultats obtenus.
LSpline := LBGRAMask.ComputeClosedSpline(LPts, ssVertexToSide);Nous verrons ainsi ce que signifie tel ou tel paramètre. Nous vérifierons dans le même temps que les images obtenues ne couvrent pas entièrement l'image d'origine.
Voici par exemple un instantané pris avec l'option ssCrossing :
Il est manifeste que la courbe finale « traverse » la courbe d'origine (le rectangle) !
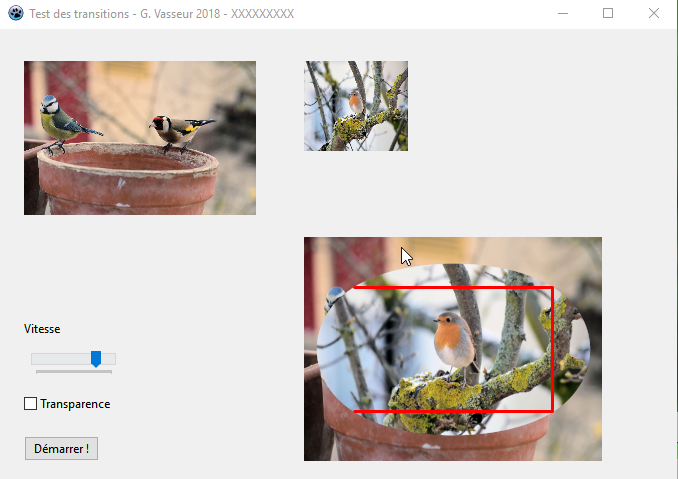
Avec l'option ssVertexToSide, nous obtenons bien entendu une disposition différente :
Cette fois-ci les pointes du rectangle se confondent avec des points de la courbe.
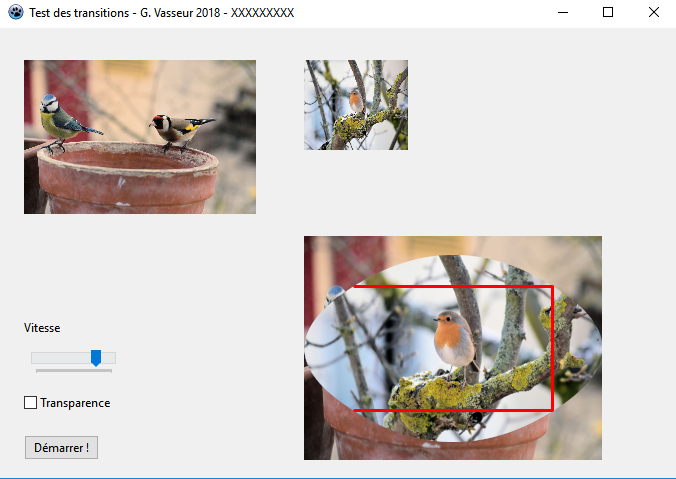
Avec l'option ssOutside, voici ce que nous obtenons :
La courbe est un peu moins allongée et plus douce encore que la précédente.
Avec ssInside, le dessin est modifié comme ceci :
Il est cette fois-ci bien circonscrit à une zone plus petite que le rectangle de repère et ressemble davantage à un médaillon.
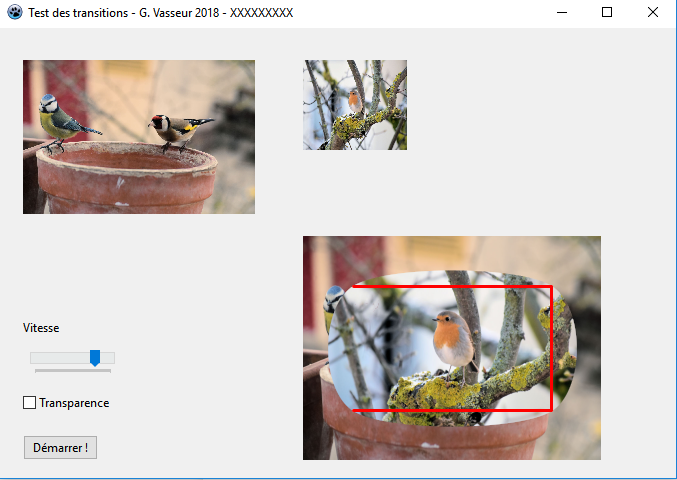
Enfin, avec ssRoundOutside, nous obtenons une courbe aux arrondis intermédiaires entre ssVertexToSide et ssOutside :
L'intérêt de ces options paraît limité pour les transitions, mais il est utile de les connaître afin d'obtenir la courbe la plus proche possible de ce qui est attendu. En ce qui concerne notre travail, il faudra surtout prendre garde au fait que ces courbes, tout comme les ellipses déjà étudiées, ne sont pas totalement couvrantes si nous nous bornons à faire varier nos coordonnées entre 0 et la largeur ou la hauteur de l'image de résultat. Par conséquent, soit nous accepterons qu'une partie de l'image d'origine ne soit pas recouverte, soit nous augmenterons la taille de l'image de destination, perdant ainsi du temps pour prolonger son dessin hors de la surface visible.
III. Conclusion▲
Avec ce tutoriel s'achève la longue série des transitions obtenues essentiellement à partir de masques et de translations, avec une pointe de splines pour une meilleure saveur ! Avant de nous lancer dans la construction d'un composant regroupant tout ce que vous avez étudié, vous aurez encore un détour à faire du côté des rotations et des homothéties. Ce sera l'objet du prochain épisode et l'occasion de découvrir d'autres classes et méthodes de BGRABitmap.
Mes remerciements vont à Alcatîz et à BeanzMaster pour leur relecture technique et à f-leb pour la correction orthographique.