I. Les transitions de recouvrement▲
Les programmes de test sont présents dans le répertoire exemples accompagnant le tutoriel.
Nous appellerons transitions de recouvrement les transitions qui affichent une image d'origine qui doit être peu à peu recouverte par l'image de destination. Ces transitions sont simples d'un point de vue mathématique puisqu'elles ne mettent en œuvre que des translations.
Pour rappel, une translation en mathématique est une transformation géométrique qui correspond à l'idée intuitive de glissement. Elle est facile à réaliser, car elle ne déforme pas l'objet translaté et par définition n'utilise pas de rotations.
Pour nommer les méthodes chargées de les effectuer, nous adopterons une convention simple : le nom de la méthode indiquera toujours le type de transition (ici over pour recouvrement) suivi de la direction du mouvement. Par exemple, pour une transition partant du coin supérieur gauche et allant vers la droite et le bas, nous implémenterons la méthode OverBottomRight.
I-A. Le recouvrement OverDown▲
[Exemple BGRABitmap 04]
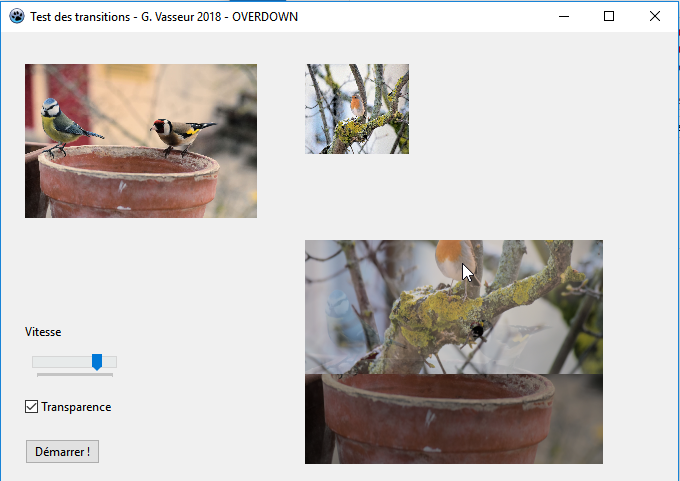
Le recouvrement OverDown nous servira à comprendre les calculs nécessaires à la série de transitions de recouvrement. L'idée fondamentale qui sous-tend tout recouvrement est celle-ci : nous dessinons l'image d'origine sur laquelle vient s'inscrire une partie de l'image de destination.
En fait, nous n'aurons pas à nous préoccuper du calcul de la partie visible de l'image de destination, car c'est le composant TPaintBox d'accueil qui s'occupera lui-même de la définir en fonction de sa surface d'affichage propre. Notre travail se réduira à fournir les coordonnées du coin supérieur gauche de l'image de destination, suivant le pourcentage réalisé de la transition. Autrement dit, nous fixerons au départ les coordonnées du point supérieur gauche de l'image de transition de telle manière qu'elle soit invisible et ce n'est que progressivement qu'elle entrera par translation dans le cadre de visibilité.
La translation conservant les longueurs et les angles, un seul point est nécessaire aux calculs. Si nous parvenons par exemple à calculer les coordonnées du point supérieur gauche de l’image, le rectangle qu'elle forme sera reproduit à l'identique à la nouvelle position.
Voici comment se présentent au départ les deux images avec la méthode OverDown :
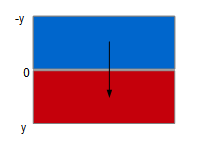
Le rectangle rouge représente l'image d'origine, mais aussi la surface visible en permanence. Le rectangle bleu représente l'image de destination. Au démarrage, nous la situerons au-dessus de l'image de destination, donc hors de la zone d'affichage, puis nous la ferons glisser par translation vers le bas.
Nous remarquons que seules les ordonnées des points de l'image de destination sont affectées par la translation. En effet, le rectangle bleu n'a pas à se déplacer vers la gauche ou la droite. Par conséquent, le calcul des coordonnées du point supérieur gauche de l'image de destination exclura l'abscisse (qui restera constante) pour définir l'ordonnée par un calcul rudimentaire.
Dans une image, nous savons que le coin supérieur gauche a pour coordonnées (0, 0). Dans notre méthode OverDown, nous laisserons donc LX à sa valeur de 0. L'image de destination étant située au-dessus de l'image d'origine, l'ordonnée de son point supérieur gauche sera négative : plus exactement, elle vaudra la valeur négative de la hauteur du rectangle qu'elle forme. Cette hauteur nous est fournie par la méthode ClientHeight de l'image d'affichage du résultat.
Pour le déplacement, nous partirons de cette valeur -ClientHeight pour lui ajouter progressivement un pourcentage d'elle-même, suivant l'étape en cours de la transition, soit ClientHeight * fStep div 100. Ainsi, l'ordonnée va se rapprocher de plus en plus de 0 et finalement l'image de destination recouvrira totalement l'image d'origine.
Voici la ligne de code à inclure dans le gestionnaire OnClick du bouton pour obtenir l'effet désiré :
LX:= 0;
[…]
LY := - imgResult.ClientHeight + imgResult.ClientHeight * fStep div
100; // OVERDOWN
Nous reconnaissons là l'unique transition utilisée lors de nos essais. Nous transformerons cette ligne de code en méthode quand nécessaire. Pour le moment, nous nous contenterons d'insérer et d'effacer les lignes de code utiles au fur et à mesure de nos besoins.
I-B. Le recouvrement OverUp▲
Le recouvrement OverUp ressemble à s'y méprendre à celui qui vient d'être vu. Simplement, il faut à présent placer l'image de destination plus bas que celle d'origine pour la faire remonter peu à peu.
La configuration de départ est celle-ci :
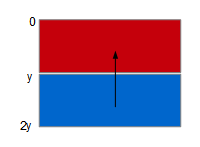
Encore une fois, les abscisses ne sont pas affectées si bien que la variable LX conservera sa valeur nulle. En revanche, l'ordonnée de départ du point supérieur gauche de l'image de destination est désormais de y. Il faut donc la décrémenter jusqu'à ce qu'elle atteigne la valeur 0 attendue.
Voici la ligne de code à inclure dans le gestionnaire OnClick du bouton pour obtenir l'effet désiré :
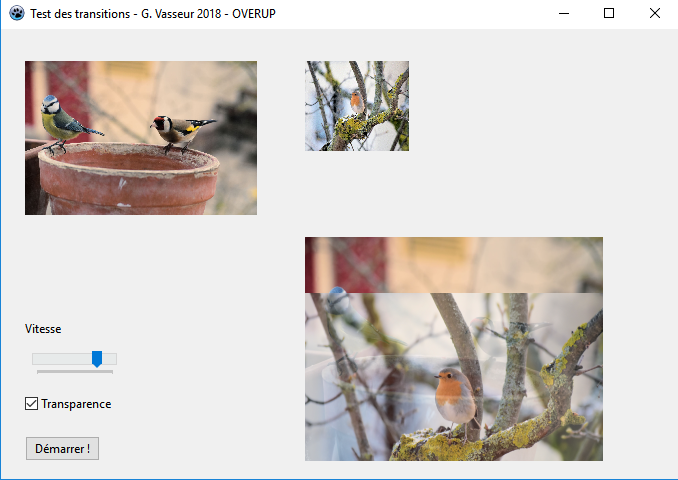
LY := imgResult.ClientHeight - imgResult.ClientHeight * fStep div 100; // OVERUPUne copie de l'interface de l'application d'essai correspondant à ce recouvrement a donné ceci :
I-C. Le recouvrement OverRight▲
Le recouvrement OverRight correspond à un autre cas de figure aussi facile à comprendre que les précédents. En effet, ce ne sont pas les ordonnées qui seront modifiées, mais les abscisses. LY sera donc laissée à une valeur constante nulle et c'est la variable locale LX qui devra s'adapter en fonction du temps.
Le schéma de fonctionnement est le suivant :
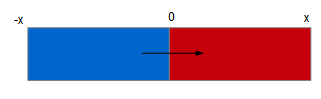
Partant de -x, l'abscisse du point supérieur gauche de l'image de destination devra atteindre 0, donc augmenter progressivement. Nous savons par ailleurs que la largeur de la zone d'affichage est fournie par la méthode ClientWidth de l'image du résultat. La formule retenue sera par conséquent :
LX := -imgResult.ClientWidth + imgResult.ClientWidth * fStep div
100; // OVERRIGHTUn affichage tel que celui-ci devrait être obtenu :
I-D. Le recouvrement OverLeft▲
Le recouvrement OverLeft, sans surprise, inverse les valeurs utilisées précédemment.
Son schéma de fonctionnement est celui-ci :
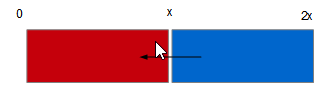
Partant de x, l'abscisse du point supérieur gauche de l'image de destination devra atteindre 0, donc diminuer progressivement. La formule retenue sera par conséquent :
LX := imgResult.ClientWidth - imgResult.ClientWidth * fStep div
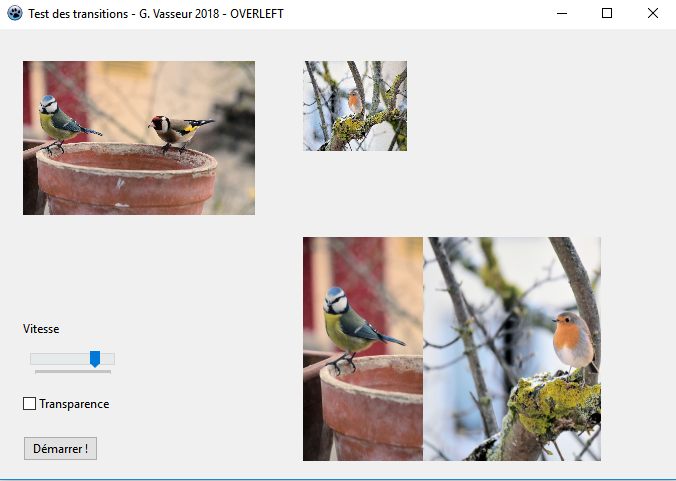
100; // OVERLEFTUn instantané de l'application pourra donner :
I-E. Le recouvrement OverBottomRight▲
[Exemple BGRABitmap 05]
Le recouvrement OverBottomRight, comme ceux qui suivent, utilise une diagonale pour la translation. Cela signifie simplement qu'il faut modifier dans le même mouvement les variables locales LX et LY.
OverBottomRight suivra le schéma ci-après :
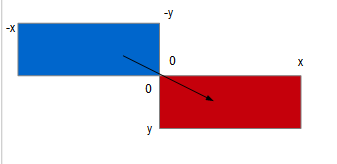
Nous voyons clairement que l'abscisse doit passer de -x à 0 et que l'ordonnée doit suivre la même progression en passant de -y à 0. Ces mouvements se traduisent ainsi pour le code :
LX := -imgResult.ClientWidth + imgResult.ClientWidth * fStep div 100; // OVERBOTTOMRIGHT
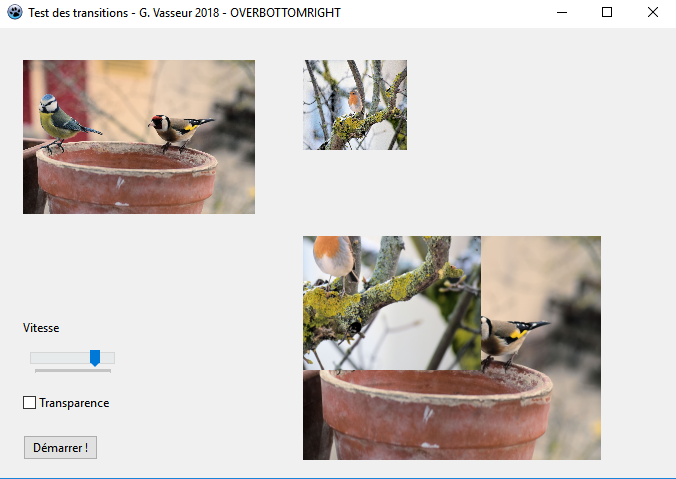
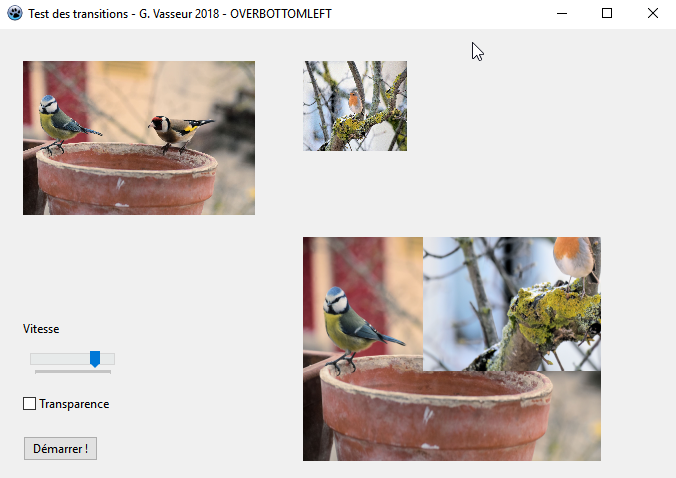
LY := -imgResult.ClientHeight + imgResult.ClientHeight * fStep div 100;Une étape de l'affichage correspondra alors à l'écran suivant :
Rien de plus simple, n'est-ce pas ?
I-F. Le recouvrement OverBottomLeft▲
Nous devinons aisément que OverBottomLeft sera très proche de ce que nous venons de traiter.
Comme d'habitude, le schéma de la translation désirée nous éclairera sur les calculs à effectuer :
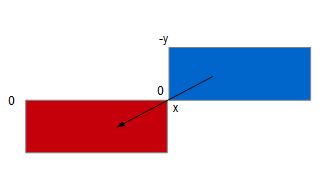
Il nous faut donc passer de x à 0 et de -y à 0, c'est-à -dire décrémenter l'abscisse tout en incrémentant l'ordonnée. La traduction en code est immédiate :
LX := imgResult.ClientWidth - imgResult.ClientWidth * fStep div 100; // OVERBOTTOMLEFT
LY := -imgResult.ClientHeight + imgResult.ClientHeight * fStep div 100;L'instantané suivant de l'écran donne une idée de l'effet obtenu :
I-G. Le recouvrement OverTopRight▲
En continuant notre exploration des transitions de recouvrement par simple translation, nous chercherons à viser le haut à droite de l'image, ce qui se traduira par le schéma :
L'analyse des données fournies par ce schéma montre que le recouvrement OverTopRight doit passer de -x à 0 pour l'abscisse et de y à 0 pour l'ordonnée.
Le code devient alors :
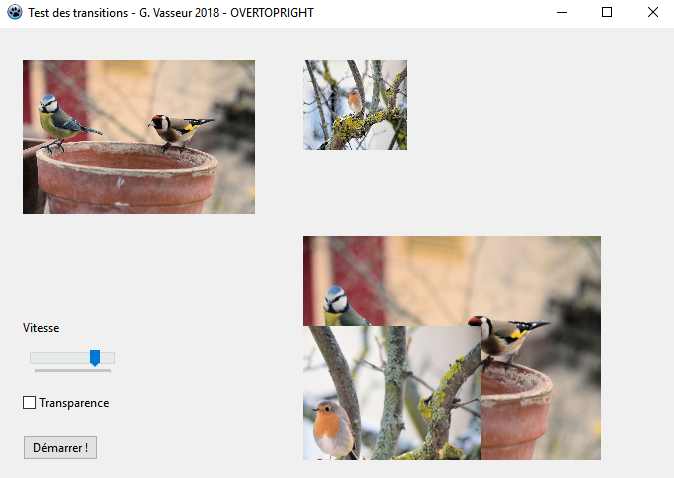
LX := -imgResult.ClientWidth + imgResult.ClientWidth * fStep div 100; // OVERTOPRIGHT
LY := imgResult.ClientHeight - imgResult.ClientHeight * fStep div 100;Une copie d'écran confirme la justesse de notre raisonnement et de nos calculs :
I-H. Le recouvrement OverTopLeft▲
L'ultime recouvrement que nous programmerons consiste à effectuer une translation vers le haut à gauche de l'image. Ce recouvrement sera nommé OverTopLeft. Son schéma correspondra à  :
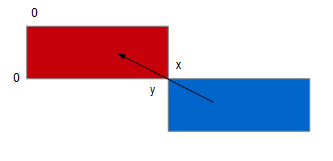
On y lit que l'abscisse doit décroître de x à 0 tout comme l'ordonnée qui doit passer de y à 0. Le code à écrire sera donc :
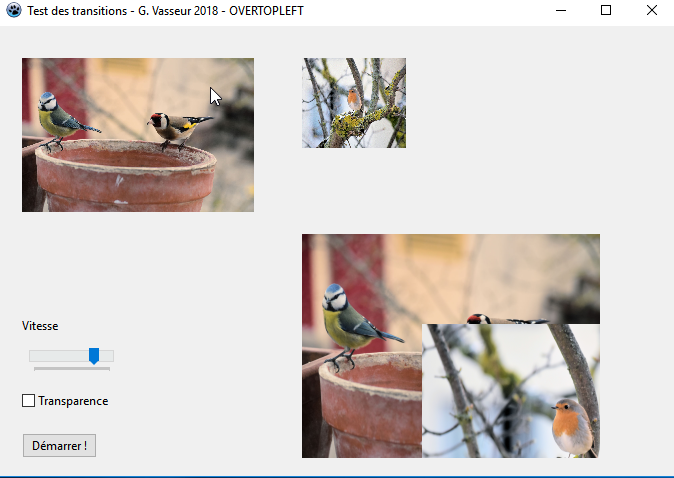
LX := imgResult.ClientWidth - imgResult.ClientWidth * fStep div 100; // OVERTOPLEFT
LY := imgResult.ClientHeight - imgResult.ClientHeight * fStep div 100;Une copie d'écran confirmera encore une fois que nous sommes sur la bonne voie :
Avec cette transition, nous avons terminé notre exploration des translations simples. Nous devons surtout retenir que quelques méthodes ont suffi pour obtenir ces résultats somme toute plutôt encourageants :
- Create et Free pour la création et la destruction des objets de dessin propres à la bibliothèque BGRABitmap ;
- Resample pour redéfinir les dimensions d'une image et donc normaliser la taille des différentes images de travail ;
- Fill pour remplir une surface de dessin ;
- PutImage pour dessiner un objet de type TBGRABitmap sur un autre de même type, avec prise en compte de la transparence ;
- Draw pour dessiner un objet de type TBGRABitmap sur le canevas d'un contrôle par exemple.
La suite permettra de compléter cette liste au fur et à mesure de nos besoins : pour cela, nous devrons créer des transitions plus complexes.
II. Pousser des images hors du champ d'affichage▲
[Exemple BGRABitmap 06]
Pour le moment, nous allons nous contenter d'explorer d'autres possibilités tout aussi faciles à mettre en œuvre que celles précédemment étudiées. Cependant, il nous faudra modifier la méthode OnClick du bouton, car ce gestionnaire suppose que l'image d'origine est immobile, ce qui n'est pas une obligation et même parfois une gêne.
Modifions donc légèrement cette méthode :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
var
LBGRATemp: TBGRABitmap;
LY, LX: Integer;
begin
btnGo.Enabled := False;
LBGRATemp := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
fStep := 0;
repeat
LX := 0;
LY := 0;
Inc(fStep);
LBGRATemp.Fill(BGRABlack);
// traitement 1 ici (source)...
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);
LBGRATemp.Draw(imgResult.Canvas, 0, 0);
Application.processMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRATemp.Free;
btnGo.Enabled := True;
end;
end;Simplement en transformant les constantes nulles du premier PutImage en variables locales, nous autorisons des modifications de l'image d'origine.
Après traitement, si nous avons modifié LX ou LY, il faut bien entendu les remettre à 0 au cas où elles ne seraient pas recalculées par la suite. Cette nécessité explique le déplacement de leur mise à zéro dans le cœur même de la boucle.
Notre application modèle est désormais adaptée à une série de nouvelles transitions dont nous allons explorer certaines ci-après.
II-A. Pousser avec PushRight▲
Une transition courante et intéressante consistera à pousser vers la sortie d'écran l'image d'origine à l'aide de l'image de destination. En nous aidant de nos habituels schémas, nous nous rendons vite compte qu'il s'agit d'appliquer la même translation aux deux images : seules leurs coordonnées respectives différeront.
Examinons par exemple le schéma applicable à PushRight qui, comme son nom l'indique, aura pour fonction de pousser l'image d'origine vers la droite :
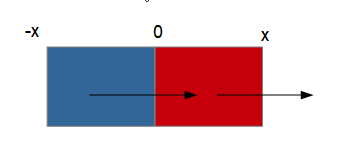
Nous voyons qu'il y a deux traitements à réaliser. L'image d'origine voit l'abscisse de son point supérieur gauche passer de 0 à x, tandis que l'image de destination voit la même abscisse passer de -x à 0. Les deux images ayant les mêmes dimensions grâce à Resample, les translations donneront l'illusion que l'image de destination pousse celle d'origine.
Le code prendra cette forme :
// traitement 1 ici (source)...
LX := imgResult.ClientWidth * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LX := -imgResult.ClientWidth + imgResult.ClientWidth * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);LY n'a pas à être modifiée. LX n'a pas la même valeur selon l'image traitée, mais elle progresse de la même façon.
Vous avez certainement noté que cette transition reprend le code de la transition OverRight. Dans notre travail final, nous tiendrons compte de ces redites pour éviter du code redondant. Pour le moment, nous ne cherchons pas l'efficacité, mais seulement à comprendre comment fonctionnent les transitions, même si elles sont élémentaires.
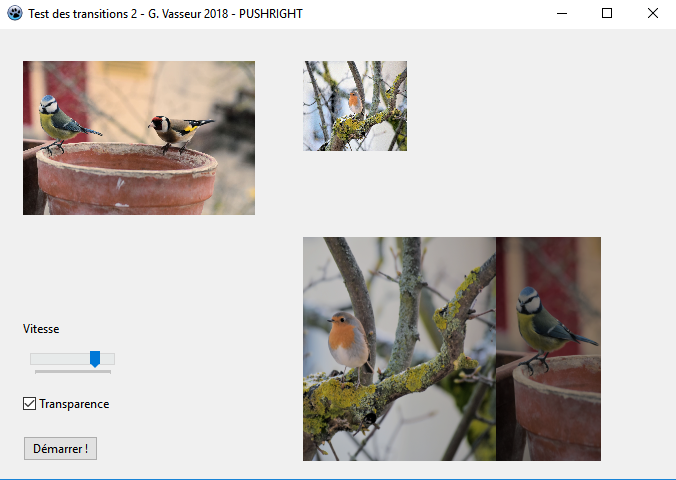
Voici une copie d'écran obtenue lors d'une étape de la transition :
Un aspect intéressant de notre travail préparatoire sur l'opacité est que l'image qui arrive devient de plus en plus lumineuse alors que celle qui disparaît semble s'évanouir dans le sombre. Bien sûr, cette remarque n'est pertinente que si la transparence a été activée avec la case à cocher !
Arrivé à ce stade du travail, il sera sans doute utile que vous cherchiez par vous-même les formules à appliquer. N'hésitez pas à faire un schéma pour éviter de vous tromper dans les coordonnées d'origine et de destination !
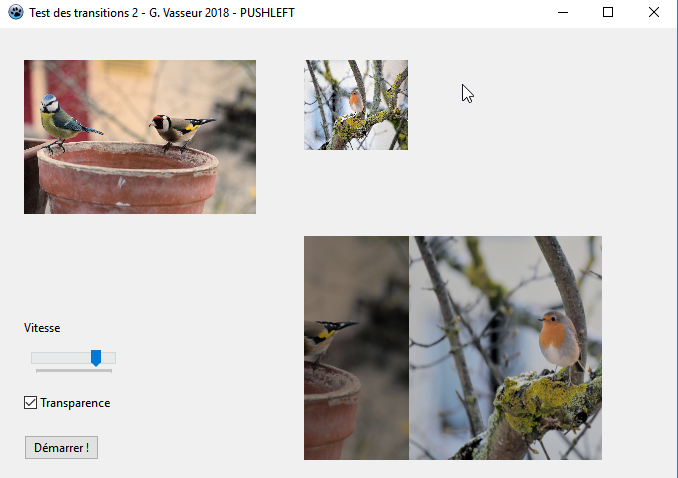
II-B. Pousser avec PushLeft▲
PushLeft fonctionne dans le sens inverse de sa consœur PushRight. Son schéma est donc :
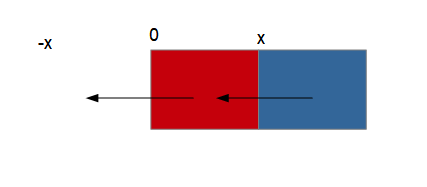
L'image d'origine doit être translatée vers la gauche avec un point supérieur gauche d'abscisse passant de 0 à -x. Dans le même temps, le point supérieur de l'image de destination verra son abscisse passer de x à 0.
Voici le code correspondant :
// traitement 1 ici (source)...
LX := - imgResult.ClientWidth * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LX := imgResult.ClientWidth - imgResult.ClientWidth * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);La copie d'écran proposée est la suivante :
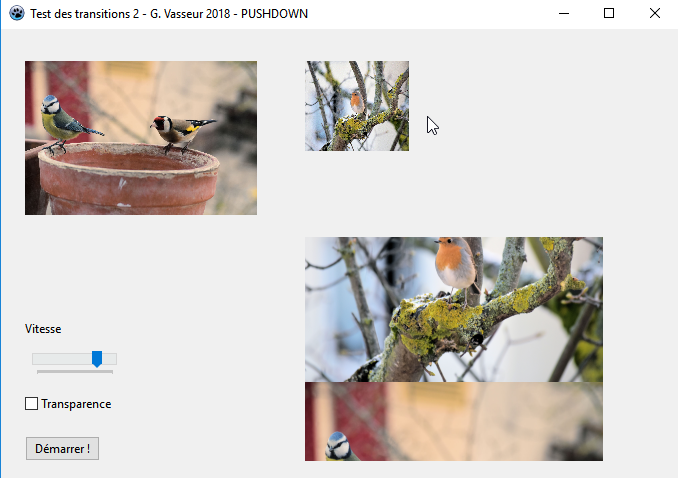
II-C. Pousser avec PushDown▲
Avec PushDown, ce sont les ordonnées qui vont être affectées selon le schéma ci-après :
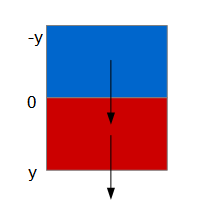
L'ordonnée du point supérieur gauche de l'image d'origine doit passer de 0 à y tandis que celle du point supérieur gauche de l'image de destination passera de -y à 0.
Voici le code correspondant :
// traitement 1 ici (source)...
LY := imgResult.ClientHeight * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LY := -imgResult.ClientHeight + imgResult.ClientHeight * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);La copie d'écran proposée est la suivante :
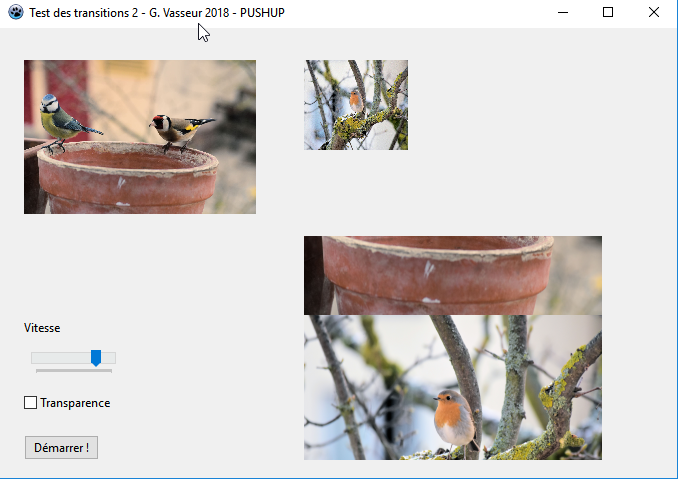
II-D. Pousser avec PushUp▲
PushUp offre la configuration inverse : l'ordonnée du point supérieur gauche de l'image d'origine doit passer de 0 à -y tandis que celle de l'image de destination passera de y à 0.
Le schéma qui lui est associé est évident :
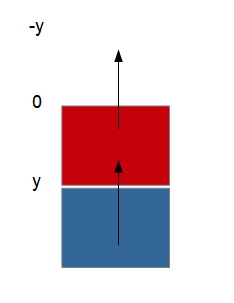
Voici le code correspondant :
// traitement 1 ici (source)...
LY := -imgResult.ClientHeight * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LY := imgResult.ClientHeight - imgResult.ClientHeight * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);La copie d'écran proposée est la suivante :
III. L'imagination au pouvoir▲
Il ne faudrait pas croire que les transitions qui ne demandent qu'une ligne de calcul sans utiliser des procédés plus complexes comme les calques soient limitées à une poignée de déplacements triviaux. Les quelques exemples qui suivent montrent qu'il n'en est rien et qu'un peu d'imagination permet de rapidement élargir sa palette d'outils !
III-A. L'inversion des images de travail▲
[Exemple BGRABitmap 07]
Une première idée est d'inverser l'image d'origine et celle de destination. Ainsi, nous obtenons facilement des transitions de découvrement en lieu et place de celles de recouvrement !
Comme exemple, nous pouvons fournir le code suivant :
// traitement 2 devenu 1 ici (destination)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmSet, Opacity);
// traitement 1 devenu 2 ici (source)...
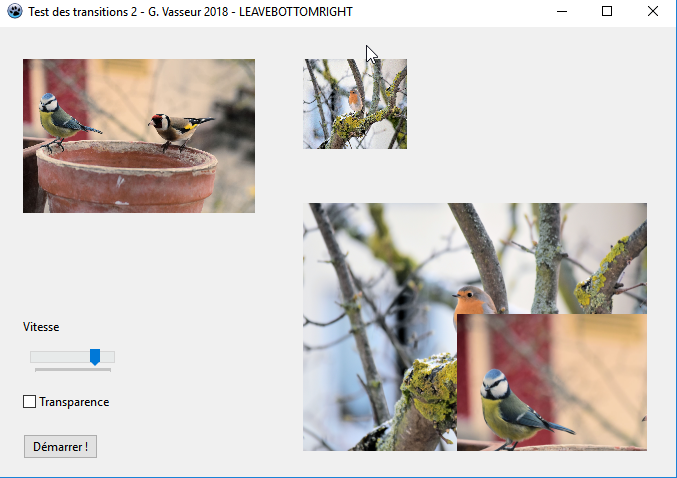
LX := imgResult.ClientWidth * fStep div 100; // LEAVEBOTTOMRIGHT
LY := imgResult.ClientHeight * fStep div 100;
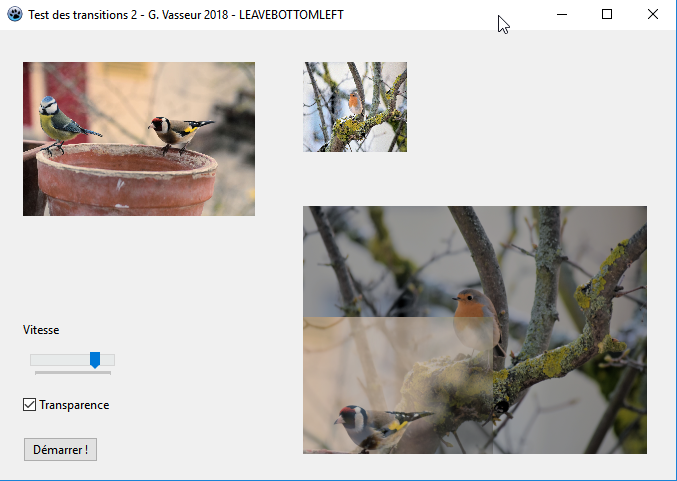
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));Nous dessinons tout d'abord l'image de destination sur laquelle nous dessinons avec un décalage de plus en plus grand l'image d'origine. Cette dernière paraît ainsi quitter l'écran en découvrant celle qui nous intéresse. Il s'agit de l'inverse de OverBottomRight, une transition que nous pourrions baptiser LeaveBottomRight.
Si vous voulez vous entraîner, vous pouvez transcrire les transitions que nous avions regroupées sous la bannière du recouvrement, multipliant ainsi les transitions à votre disposition.
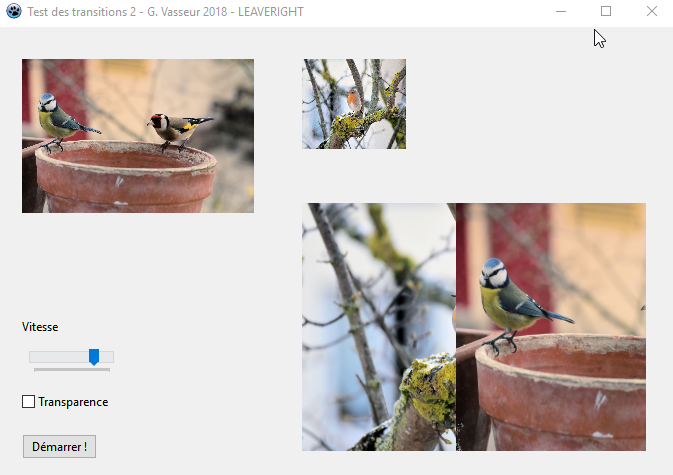
Une copie d'écran a pu donner ceci :
Voici le code pour LeaveRight :
// traitement 2 devenu 1 ici (destination)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmSet, Opacity);
// traitement 1 devenu 2 ici (source)...
LX := imgResult.ClientWidth * fStep div 100; // LEAVERIGHT
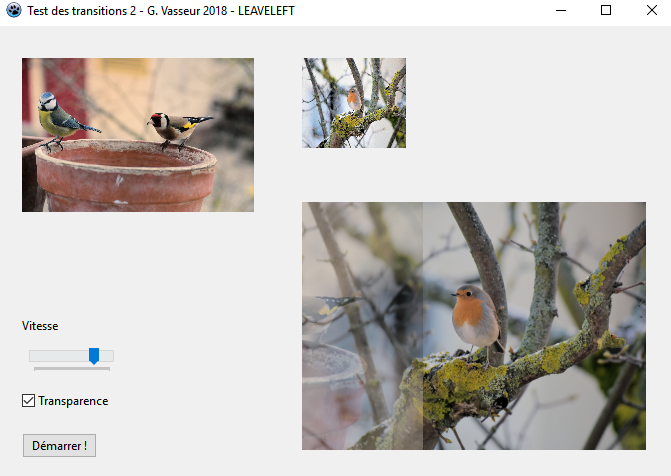
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
Voici celui pour LeaveLeft :
// traitement 2 devenu 1 ici (destination)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmSet, Opacity);
// traitement 1 devenu 2 ici (source)...
LX := -imgResult.ClientWidth * fStep div 100; // LEAVELEFT
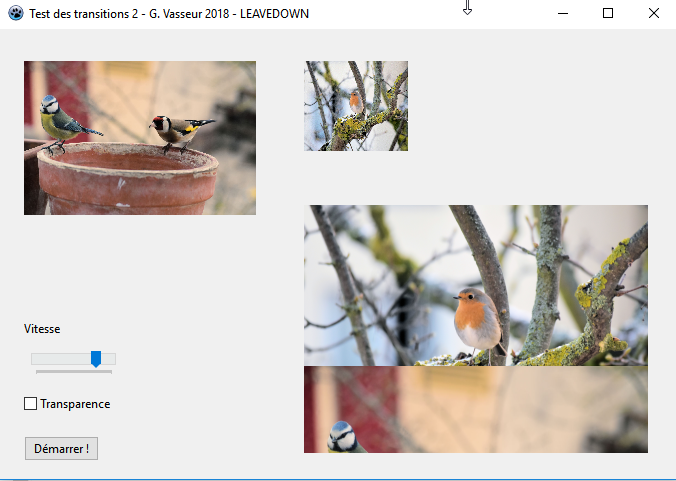
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
Voici le code pour LeaveDown :
// traitement 2 devenu 1 ici (destination)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmSet, Opacity);
// traitement 1 devenu 2 ici (source)...
LY := imgResult.ClientHeight * fStep div 100; // LEAVEDOWN
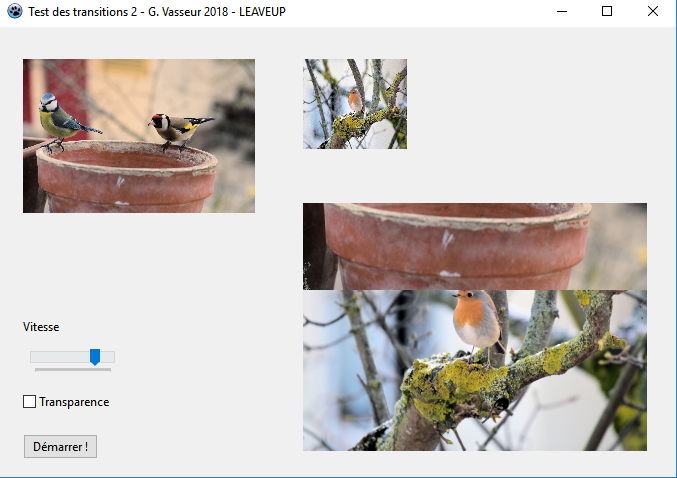
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
Voici celui pour LeaveUp :
// traitement 2 devenu 1 ici (destination)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmSet, Opacity);
// traitement 1 devenu 2 ici (source)...
LY := -imgResult.ClientHeight * fStep div 100; // LEAVEUP
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
Voici le code pour LeaveBottomLeft :
// traitement 2 devenu 1 ici (destination)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmSet, Opacity);
// traitement 1 devenu 2 ici (source)...
LX := -imgResult.ClientWidth * fStep div 100; // LEAVEBOTTOMLEFT
LY := imgResult.ClientHeight * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
Voici le code pour LeavetTopRight :
// traitement 2 devenu 1 ici (destination)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmSet, Opacity);
// traitement 1 devenu 2 ici (source)...
LX := imgResult.ClientWidth * fStep div 100; // LEAVEBOTTOMRIGHT
LY := -imgResult.ClientHeight * fStep div 100;
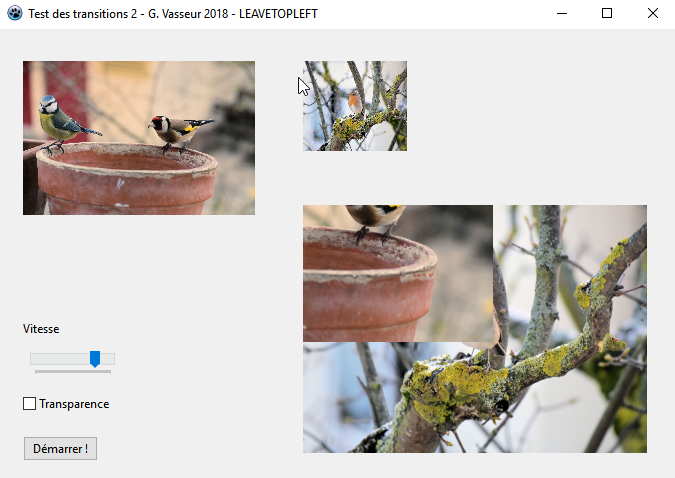
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
Enfin, voici le code pour LeaveTopLeft :
// traitement 2 devenu 1 ici (destination)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmSet, Opacity);
// traitement 1 devenu 2 ici (source)...
LX := -imgResult.ClientWidth * fStep div 100; // LEAVETOPLEFT
LY := -imgResult.ClientHeight * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmDrawWithTransparency, Opacity(False));
Les calculs mettent essentiellement en jeu un bon repérage des coordonnées à modifier (l'abscisse, l'ordonnée, l'abscisse et l'ordonnée simultanément) et des signes algébriques adaptés devant les expressions de déplacement. Bien sûr, ces transitions sont un peu répétitives et n'apportent pas d'éléments nouveaux du point de vue de la programmation, mais l'utilisateur final sera sans doute satisfait d'en avoir autant à sa disposition !
Peu élégante, l'inversion des images peut être évitée grâce à d'autres techniques. Nous pouvons par exemple considérer que nous faisons disparaître peu à peu l'image d'origine et que celle de destination a une partie masquée qui correspond exactement à celle visible de l'image d'origine. Nous explorerons cette technique dans les tutoriels suivants.
III-B. Les fonctions trigonométriques▲
Les fonctions trigonométriques sont d'autres outils qui produisent des effets intéressants. Nous pouvons par exemple nous appuyer sur le fait que la valeur retournée par des fonctions comme le sinus ou le cosinus est comprise entre 0 et 1 pour certaines plages de valeurs fournies en entrée, ce qui autorise des jeux simples avec le pourcentage de réalisation d'une transition. Le déphasage de ϖ/2 de ces fonctions peut lui aussi être source d'effets.
[Exemple BGRABitmap 08]
Dans l'exemple suivant, nous obtenons un équivalent de OverTopLeft, mais avec une courbe arrondie du meilleur effet :
// traitement 1 ici (source)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LY := imgResult.ClientHeight - Round(sin(fStep * pi / 200) * imgResult.ClientHeight);
LX := Round(cos(fStep * pi / 200) * imgResult.ClientWidth);
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);Les fonctions sin et cos de Lazarus attendent un paramètre en radians : si vous utilisez des mesures en degrés, il faut penser à leur conversion ! Pour convertir les degrés en radians, on multiplie la mesure de l'angle par ϖ puis on divise le résultat par 180 degrés. De plus, les valeurs attendues pour les coordonnées sont des entiers, d'où la nécessité d'employer la fonction Round pour arrondir les valeurs calculées.
Examinons la première formule, qui concerne LY. Comme fStep varie de 0 à 100, le paramètre associé à la fonction sin variera de 0 à π/2. Le sinus de 0 vaut 0 et celui de π/2 vaut 1 : le sinus variera donc de 0 à 1, selon une pente positive monotone (de plus, non linéaire, ce qui nous intéresse au plus haut point !). Finalement, grâce à la soustraction, LY variera de ClientHeight à 0, ce qui remontera bien notre image jusqu'à la faire disparaître vers le haut. Sachant que le cosinus de 0 vaut 1 et que celui de π/2 vaut 0, un raisonnement similaire montrerait que LX variera de ClientWidth à 0 selon une pente négative monotone (et encore une fois non linéaire !).
Voici une courte vidéo de cette transition (appelée OverTopLeftSinCos1) en action :
[Exemple BGRABitmap 09]
Une partie des calculs peut rester linéaire, une seule fonction trigonométrique étant alors utilisée. Voici un exemple de la variante OverTopRightSin de OverTopRight avec l'ordonnée de l'image de destination traitée avec un sinus :
// traitement 1 ici (source)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LY := imgResult.ClientHeight - Round(sin(fStep * pi / 200) * imgResult.ClientHeight);
LX := -imgResult.ClientWidth + imgResult.ClientWidth * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);C'est encore un déplacement arrondi qui est produit, surtout visible en fin de transition. La vidéo suivante montre l'effet obtenu :
[Exemple BGRABitmap 10]
Nous pouvons même prévoir que l'image de destination parte d'un bord du contrôle d'accueil et décrive une portion de la courbe sinusoïdale prévue. Voici le code de OverLeftDownUpSin qui utilise cette possibilité :
// traitement 1 ici (source)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LY := Round(sin(fStep * pi / 100) * imgResult.ClientHeight);
LX := imgResult.ClientWidth - imgResult.ClientWidth * fStep div 100;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);La transition en action produit cet effet :
[Exemple BGRABitmap 11]
Un dernier exemple de code montre un autre déplacement original avec une combinaison de fonctions trigonométriques simples :
// traitement 1 ici (source)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
// traitement 2 ici (destination)...
LX := round(imgResult.ClientWidth * sin(fStep * pi / 100));
LY := round(imgResult.ClientHeight * cos(fStep * pi / 200));
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);Afin de mieux visualiser l'effet obtenu, la courte vidéo qui suit montre la transition OverTopLeftSinCos en action :
III-C. Un soupçon de paraboles pour les rebonds▲
[Exemple BGRABitmap 12]
Dans le même esprit de découverte, les paraboles offrent des variantes de transitions qui évoqueront les rebonds d'un objet élastique sur le sol (bouncing). Comme nous connaissons au moins les coordonnées du premier point d'où doit démarrer notre animation (il s'agira par exemple du coin inférieur gauche du contrôle graphique qui affiche le résultat de notre transition à un instant donné) et que nous pouvons décider de même du sommet de notre parabole, en fait de la hauteur du rebond, son équation est assez facilement déterminable.
Prenons un point A de coordonnées (0, 0) et un point S de coordonnées (sx, sy). Si notre parabole passe par A et par S et que S est son sommet, l'équation de la parabole peut être donnée sous la forme : y = a * (x – sx)² + sy. Pour déterminer le coefficient a, il suffit d'utiliser les coordonnées du point connu A qui obéiront à l'équation : 0 = a * (0 – sx)² + sy.
Nous en tirons : a = - sy / sx², d'où y = - sy / sx² * (x – sx)² + sy.
Comme nous allons avoir besoin de la fonction power pour le calcul de formules au carré, nous ajoutons tout de suite l'unité math dans la partie implementation de l'unité :
implementation
uses
math;Le code correspondant n'est pas très compliqué à comprendre si ce n'est qu'il faut prendre garde au fait que nous utilisons dans notre programme un pourcentage des dimensions et qu'il faut par conséquent en tenir compte dans nos calculs. De même, il faut faire attention à ce que l'origine des calculs soit bien le point d'abscisse 0 ou de la ramener à lui si nécessaire (c'est le rôle de la variable AOffset).
Le schéma ci-après montre une étape du déplacement de l'image en suivant le dessin de cinq paraboles de plus en plus petites pour mimer un amortissement des rebonds :
C'est le point inférieur droit de l'image qui est choisi ici pour les déplacements, mais ces déplacements sont exactement les mêmes que ceux du point supérieur gauche puisqu'il s'agit encore une fois d'une série de translations qui conservent les formes géométriques. Pour obtenir les rebonds, il suffit que le point choisi parcoure le tracé de toutes les paraboles.
Nous allons déclarer une méthode Parabola dans la partie de la fiche principale :
procedure SetSpeed(AValue: Byte);
procedure SetWithOpacity(AValue: Boolean);
function Parabola(AOffset, AMax, APerCent: Integer): Integer; // nouveau
public
function Opacity(Up: Boolean = True): Byte;Après avoir positionné le curseur dans la classe de la fiche, pour créer le squelette de cette méthode nous utilisons la combinaison de touches Ctrl-Maj-C. Ensuite, nous tapons ce qui suit :
function TMainForm.Parabola(AOffset, AMax, APerCent: Integer): Integer;
// *** parabole ***
var
LL: Real;
begin
LL := (AMax - AOffset) * imgResult.ClientWidth / 100;
Result := Round((-imgResult.ClientHeight * APerCent / 100 / power(LL, 2)) *
power((imgResult.ClientWidth * (fStep - AOffset) div 100) - LL, 2) +
imgResult.ClientHeight * APerCent div 100);
end;En fournissant la distance entre l'abscisse du premier point coupant l'axe des x et l'origine de cet axe (AOffset), l'abscisse du sommet de la parabole (AMax) et le pourcentage désiré de rebond (APerCent), nous avons tous les éléments nécessaires au calcul de l'équation de la parabole et donc des ordonnées correspondant au point de l'image à déplacer.
Afin d'imiter des rebonds, nous choisissons de soumettre l'image de destination à la fonction qui vient d'être définie avec cinq équations différentes pour des paraboles aux sommets de plus en plus bas et dessinées sur des distances de plus en plus courtes. C'est la variable fStep qui sert à déterminer les paramètres de la fonction :
procedure TMainForm.btnGoClick(Sender: TObject);
// *** dessin ***
var
LBGRATemp: TBGRABitmap;
LY, LX: Integer;
begin
btnGo.Enabled := False;
LBGRATemp := TBGRABitmap.Create(imgResult.ClientWidth, imgResult.ClientHeight, BGRABlack);
try
fStep := 0;
repeat
Inc(fStep);
LBGRATemp.Fill(BGRABlack);
// traitement 1 ici (source)...
LX := 0;
LY := 0;
LBGRATemp.PutImage(LX, LY, fBGRAFrom, dmSet, Opacity(False));
LX := -imgResult.ClientWidth + imgResult.ClientWidth * fStep div 100;
case fStep of
0..30: LY := - Parabola(0, 15, 80);
31..50: LY := - Parabola(30, 40, 60);
51..70: LY := - Parabola(50, 60, 50);
71..80: LY := - Parabola(70, 75, 35);
81..90: LY := - Parabola(80, 85, 20);
91..100: LY := - Parabola(90, 95, 5);
end;
LBGRATemp.PutImage(LX, LY, fBGRATo, dmDrawWithTransparency, Opacity);
LBGRATemp.Draw(imgResult.Canvas, 0, 0);
Application.ProcessMessages;
sleep(100 - fSpeed);
until fStep = 100;
finally
LBGRATemp.Free;
btnGo.Enabled := True;
end;
end;Le signe moins devant l'appel de la fonction Parabola permet de prendre en compte l'inversion de l'axe des ordonnées en informatique par rapport aux habitudes scolaires.
L'effet obtenu est plutôt spectaculaire et n'aura pas nécessité beaucoup de travail. Surtout, notre fonction s'adapte à des images de n'importe quelles dimensions, ce qui est appréciable !
Le petit film suivant va vous en convaincre :
Malgré la rédaction d'une formule plus complexe, il s'agit d'une transition qui se contente des méthodes que nous avons déjà utilisées. Là encore c'est notre imagination, accompagnée d'un peu de tâtonnement et de quelques connaissances en mathématiques, qui nous fera découvrir les possibilités insoupçonnées d'outils d'apparence rudimentaire !
IV. Conclusion▲
Avec ce tutoriel, vous aurez appris à implémenter en Pascal sous Lazarus des transitions d'image à image selon diverses techniques : par recouvrement, en poussant, par découvrement, à l'aide de fonctions trigonométriques ou paraboliques. Toutes ces techniques n'ont fait appel qu'à quelques méthodes de la bibliothèque BGRABitmap. Avec le tutoriel suivant, vous apprendrez à utiliser des masques pour des effets encore plus variés !
Mes remerciements vont à Alcatîz et à BeanzMaster pour leurs relectures techniques et à f-leb pour la correction orthographique.