IV. Les outils de programmation▲
Cette partie décrit deux outils fondamentaux pour le fonctionnement de GVLOGO : les piles et l'évaluateur d'expressions numériques.
IV-A. Les piles▲
IV-A-1. Définition▲
Une pile informatique peut être figurée par une pile d'assiettes posées sur une table : lorsque j'empile une donnée (push en anglais), je pose une assiette et lorsque je dépile une donnée (pull en anglais), je retire une assiette de la pile. La dernière donnée est donc la première à pouvoir être extraite : on parle de pile LIFO (Last In First Out = dernier entré, premier sorti). Une pile permet en fait de mémoriser les données manipulées dans l'ordre où elles seront à utiliser.
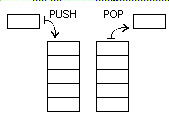
Les piles sont très utilisées par GVLOGO. Elles permettent tout à la fois de faire fonctionner l'interpréteur en stockant des données à récupérer plus tard dans un certain ordre, et d'effectuer des calculs complexes, en particulier pour l'évaluation d'expressions arithmétiques telles que (2 * 4,5) / 8. Comme la lecture d'une ligne de programme s'effectue par convention de la gauche vers la droite, si l'on rencontre une opération, rien n'indique a priori que les arguments nécessaires sont fournis : mentalement, nous découvrons les éléments au fur et à mesure de notre lecture. Un programme fait de même !
IV-A-2. Exemples▲
Les exemples qui suivent seront très détaillés. En effet, le fonctionnement d'une pile est au cœur de celui de l'interpréteur lui-même.
IV-A-2-a. Un exemple simple▲
On souhaite effectuer l'opération SOMME 24 35qui additionne les deux nombres fournis en paramètres. Pour cet exemple, on utilisera deux piles, la première contenant les données, la seconde les opérations à effectuer et le nombre de paramètres attendus.
Tout d'abord, on rencontre une opération à effectuer : ici, une addition. On sait qu'elle nécessite deux données : on empile cette opération et le nombre de paramètres attendus.
|
<pile vide> |
2 |
|
SOMME |
Ensuite, on rencontre une donnée. Afin de la mémoriser, on empile 24. SOMMEn'attend plus qu'un paramètre : on décrémente le sommet de la seconde pile :
|
24 |
1 |
|
SOMME |
On rencontre encore une donnée. On empile 35et on décrémente le sommet de l'autre pile :
|
35 |
0 |
|
24 |
SOMME |
Le 0 au sommet de la seconde pile indique que les données nécessaires sont acquises. On retire le sommet de la seconde pile pour en extraire l'opération qui peut à présent être effectuée.
|
35 |
SOMME |
|
24 |
On effectue alors l'addition sur la pile :
|
59 |
<pile vide> |
On récupère le résultat (59), par exemple pour l'afficher, et la première pile est vide.
Cette technique permet par conséquent de mémoriser des résultats intermédiaires : on peut imaginer que 35 est le résultat d'une autre opération et sa présence sur la pile fournira toujours le second élément nécessaire à l'addition initiale.
IV-A-2-b. Un exemple plus complexe▲
On souhaite à présent effectuer l'opération SOMME 24 PRODUIT 5 7, sachant que PRODUITmultiplie deux données sur la pile.
Tout d'abord, on rencontre l'opération à effectuer : ici, une addition. On sait qu'elle nécessite deux données :
|
<pile vide> |
2 |
|
SOMME |
Ensuite, on rencontre une donnée. Afin de la mémoriser, on empile 24.
SOMMEn'attend plus qu'un paramètre.
On décrémente le sommet de la seconde pile :
|
24 |
1 |
|
SOMME |
On rencontre une seconde opération qui est PRODUIT, elle-même nécessitant deux données. Il faut empiler ces informations :
|
24 |
2 |
|
PRODUIT |
|
|
1 |
|
|
SOMME |
La donnée suivante est 5, qu'on empile en décrémentant par ailleurs le sommet de l'autre pile :
|
5 |
1 |
|
24 |
PRODUIT |
|
1 |
|
|
SOMME |
On a donc une opération SOMMEpendante qui attend encore une donnée et une opération PRODUITqui elle aussi attend une donnée.
La donnée suivante est 7 qu'on empile :
|
7 |
0 |
|
5 |
PRODUIT |
|
24 |
1 |
|
SOMME |
Le 0au sommet de la seconde pile indique que l'opération pendante qui la suit a les paramètres qu'elle attend à sa disposition. On dépile ce 0devenu inutile.
|
7 |
PRODUIT |
|
5 |
1 |
|
24 |
SOMME |
On récupère alors PRODUIT. On peut donc effectuer cette opération et déposer son résultat sur le sommet de la première pile en décrémentant le sommet de la seconde pile.
|
35 |
0 |
|
24 |
SOMME |
On en a terminé avec la multiplication. La pile contient les deux données nécessaires à SOMME: on peut donc l'effectuer comme dans l'exemple 1.
Le 0 au sommet de la seconde pile indique que les données nécessaires sont acquises. On retire le sommet de la seconde pile pour en extraire l'opération qui peut à présent être effectuée.
|
35 |
SOMME |
|
24 |
On effectue alors l'addition sur la pile :
|
59 |
<pile vide> |
On récupère le résultat (59), par exemple pour l'afficher, et la première pile est vide.
Il est bien entendu que cet enchaînement d'opérations exige des éléments non encore réalisés :
- le flux du texte à exécuter doit être acquis et analysé pour en définir les éléments de base ;
- il faut pouvoir distinguer une opération d'une donnée ;
- le nombre de paramètres d'une opération doit être retrouvé pour être empilé ;
- une pile fournit au minimum les moyens d'empiler et de dépiler une donnée. D'autres opérations élémentaires sont souvent utiles : duplication de la dernière donnée, test de la profondeur de la pile, incrémentation et décrémentation du sommet… Les piles d'entiers et de réels fournissent d'autre part l'essentiel des opérations qu'on peut effectuer sur les données numériques qu'elles gèrent : addition, soustraction…
IV-A-3. Opérations sur les piles (et les queues)▲
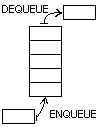
GVLOGO n'a pas pour vocation de traiter des opérations de bas niveau comme les piles, mais il en fournit cependant une structure minimale. De plus, il implémente une structure de queue : les éléments sont alors stockés les uns après les autres, et c'est le plus ancien qui est déstocké le premier.
Les primitives ci-après sont décrites dans ce chapitre, mais relèvent du traitement des listes. Elles simulent le fonctionnement d'une pile ou d'une queue à partir d'une liste.
- EMPILE: attend le nom d'une variable puis un mot ou une liste - ne renvoie rien - la primitive place le second paramètre au début de la variable qui doit être une liste.
Exemples :
EMPILE "MAPILE 124→ -
EMPILE "MAPILE 568→ -
-
SOMMET : attend le nom d'une variable en entrée - renvoie une liste ou un mot - la primitive renvoie le dernier élément stocké dans la pile indiquée par le paramètre qui doit être une liste, sans le retirer de cette dernière.
Exemple :
ECRIS SOMMET "MAPILE→ 568
-
DEPILE : attend le nom d'une variable en entrée - renvoie une liste ou un mot - la primitive renvoie le dernier élément stocké dans la pile indiquée par le paramètre qui doit être une liste, en le retirant de cette dernière.
Exemples :
ECRIS DEPILE "MAPILE→ 568
ECRIS DEPILE "MAPILE→ 124
-
QUEUE : attend une variable puis une liste ou un mot en entrée - ne renvoie rien - la primitive stocke le second paramètre dans la première liste pour former une queue.
Exemple :
QUEUE "MAQUEUE [ceci est stocké]→ -
- DEQUEUE : attend une variable en entrée - renvoie une liste ou un mot - la primitive renvoie le premier élément stocké dans une queue en le retirant de cette dernière.
Exemple :
ECRIS DEQUEUE "MAQUEUE→ un ancien élément stocké
Les notions de queue et de pile sont très souples pour GVLOGO si bien qu'il est possible de traiter n'importe quelle variable, pourvu qu'elle renvoie une liste. De plus, les primitives ENQUEUEet EMPILEsont strictement équivalentes : on peut donc empiler une donnée et traiter la liste comme une pile, une queue ou une liste ordinaire, et réciproquement !
IV-A-4. Implémentation des piles▲
L'unité GVStacks offre une classe de pile générique et les classes nécessaires pour manipuler des entiers, des réels et des chaînes de caractères.
On aura tout intérêt, si l'on utilise Delphi, à utiliser les piles fournies dans System.Generics.Collections(20). Comme Lazarus ne sait pas encore traiter les classes génériques de manière aussi satisfaisante que Delphi, la solution adoptée pour le projet est de travailler à partir d'une classe générique commune. Elle est plus limitée dans la mesure où elle ne connaît pas d'énumération. D'autre part, la notification est moins complète, Lazarus n'acceptant que les classes comme support des génériques. En revanche, plusieurs fonctionnalités intéressantes ont été ajoutées.
IV-A-4-a. Constantes▲
L'unité GVConsts a été complétée. On a fixé la taille minimale de la pile à 8, ce qui permet de ne pas réallouer en permanence de la mémoire pour l'accroissement de la pile.
De nouvelles erreurs possibles ont été par ailleurs prévues dans GVErrConsts. On retrouve ces erreurs dans les chaînes de ressources :
IE_EmptyStack = 'ERREUR INTERNE - La pile interne "%s" est vide.';
IE_OutOfMemory =
'ERREUR INTERNE - La mémoire est insuffisante pour la pile "%s".';
IE_LowStack = 'ERREUR INTERNE - Pas assez d''éléments dans la pile "%s".';On remarquera que ces erreurs sont marquées comme internes, car elles ne se produiront que si notre programme final connaît un problème de conception.
Enfin, des constantes énumérées ont été définies pour les notifications :
// *** notifications de la pile ***
// ajout, suppression, changement, effacement
TGVStackNotification = (stAdded, stRemoved, stChanged, stCleared);La première indique qu'un élément a été ajouté à la pile, la deuxième qu'un élément a été retiré, la troisième qu'un changement autre est intervenu, la dernière que la pile a été remise à zéro.
IV-A-4-b. La classe TGVSTack▲
Les piles sont implémentées en utilisant les classes génériques. Pour rappel, ces classes fournissent un modèle sur lequel viendront s'appuyer des classes spécialisées. Ainsi, à partir d'une seule classe de pile, on peut créer toutes les piles imaginables simplement en précisant le type à utiliser.
Les avantages évidents de cette méthode sur celle plus classique de définitions de classes au cas par cas sont un gain de temps, une souplesse largement accrue, une sécurité renforcée puisque le code n'a pas à être ressaisi pour chacune des classes et la possibilité de modifier le comportement de toutes les classes spécialisées à partir de la seule modification de la classe générique :
// *** pile générique ***
generic TGVStack<T> = class(TObject)Les piles spécialisées prédéfinies sont les suivantes :
// *** piles spécialisées ***
TGVIntegerStack = specialize TGVStack<Integer>;
TGVRealStack = specialize TGVStack<Real>;
TGVStringStack = specialize TGVStack<string>;
TGVDoubleStack = specialize TGVStack<Double>;
TGVExtendedStack = specialize TGVStack<Extended>;
TGVEvalStack = specialize TGVStack<TGVBaseItem>;En ce qui concerne l'interface de la classe TGVStack, en voici le listing :
// *** pile générique ***
generic TGVStack<T> = class(TObject)
private
fItems: array of T;
fError: TGVErrors; // gestionnaire des erreurs
fCount: Integer; // nombre d'éléments
fCapacity: Integer; // capacité actuelle
fOnNotify: TGVStackEvent; // notification
procedure Expand; // expansion si nécessaire
function GetCapacity: Integer; // capacité actuelle
function GetItem(N: Integer): T; // accès à un élément
procedure SetCapacity(const Value: Integer); // fixe la capacité
procedure SetItem(N: Integer; AValue: T);
protected
procedure Notify(Action: TGVStackNotification); virtual; // notification
procedure DoPush(const Value: T); // empilement
function DoPop: T; // dépilement
public
constructor Create; overload; // création
destructor Destroy; override; // destruction
procedure Clear; // nettoyage
function IsEmpty: Boolean; inline; // pile vide ?
procedure Push(const Value: T); // empilement avec notification
function Pop: T; // dépilement avec notification
function Peek: T; // sommet de la pile
procedure Drop; // sommet de la pile éjecté
procedure Dup; // duplication au sommet de la pile
procedure Swap; // inversion au sommet de la pile
procedure Over; // duplication de l'avant-dernier
procedure Rot; // rotation au sommet de la pile
procedure Shrink; // contraction de la pile
function Needed(Nb: Integer): Boolean; // nombre d'éléments désirés
property Count: Integer read fCount default 0; // compte des éléments
// capacité de la pile
property Capacity: Integer read GetCapacity write SetCapacity
default CMinStack;
// accès direct à un élément
property Item[N: Integer]: T read GetItem write SetItem; default;
// notification d'un changement
property OnNotify: TGVStackEvent read fOnNotify write fOnNotify;
// notification d'une erreur
property Error: TGVErrors read fError write fError;
end;Cette interface appelle les remarques suivantes :
- le paramètre T qui apparaît souvent sera celui remplacé par le type réel mis en œuvre par la classe spécialisée ;
- le fondement de la pile est le tableau ouvert fItemsqui verra son dernier élément pointé par le champ privé fCount;
- la notion de capacité (à travers le champ privé fCapacity) complique un peu la classe, mais permet d'accélérer les empilements en ne procédant pas sans cesse à des allocations de mémoire ;
- la propriété Itemest définie par défaut, ce qui signifie par conséquent que l'utilisateur n'a pas besoin de la spécifier (les deux écritures sont équivalentes : MaPile.Item[2]et Mapile[2]) ;
- la plupart des méthodes définies sont destinées à manipuler la pile : Push, Peek, Pop, Drop, Dup, Swap, Overet Rot. Les programmeurs en Forth reconnaîtront là des outils très familiers ;
- la présence des méthodes DoPushet DoPopse justifie par le fait que ces opérations de base sur la pile sont employées par les autres méthodes qui ne doivent déclencher l'événement OnNotifyqu'une seule fois : ce sont donc deux méthodes qui ne notifient rien, contrairement à Pushet à Pop.
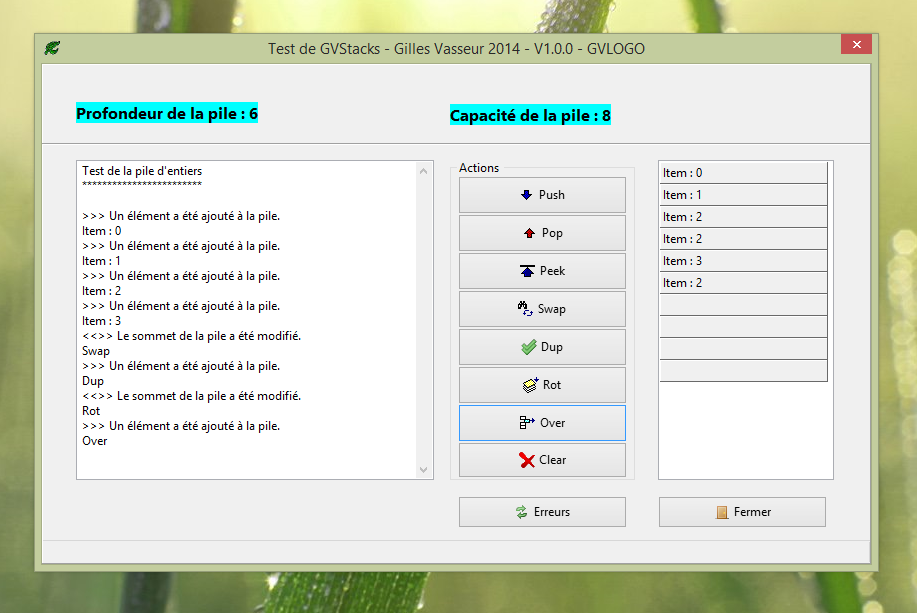
IV-A-4-c. Test de l'unité TGVStacks▲
Pour ne pas changer, le programme de test est décliné en deux versions :
- Lazarus pour Windows 32Â ;
- Lazarus pour Linux.
La méthode StackChangedexige quelques commentaires :
procedure TMainForm.StackChanged(Sender: TObject; Act: TGVStackNotification);
// changement de la pile
var
Li: Integer;
begin
for Li := 0 to fStackStr.Count - 1 do
sgStack.Cells[0,Li] := fStackStr[Li];
case Act of
stAdded : begin
mmoActions.Lines.Add('>>> Un élément a été ajouté à la pile.');
sgStack.RowCount := fStackStr.Count + 4;
end;
stRemoved : begin
mmoActions.Lines.Add('<<< Un élément a été retiré de la pile.');
sgStack.Cells[0,fStackStr.Count] := EmptyStr;
end;
stChanged : mmoActions.Lines.Add('<<>> Le sommet de la pile a été modifié.');
stCleared: begin
mmoActions.Lines.Add('000 La pile est vide.');
for Li := 0 to sgStack.RowCount -1 do
sgStack.Cells[0,Li] := EmptyStr;
end;
end;
if not fErr then // si erreur inactive
UpdateButtons;
end;Cette méthode a été affectée à la propriété OnNotifyde la pile. Elle remplit le composant TStringGridavec les éléments de la pile, répartit son travail suivant l'action notifiée et met à jour les boutons qui seront actifs ou non selon la profondeur de la pile. On remarquera la mise à jour permanente de la TStringGridafin de ne pas laisser de chaînes visibles après un dépilement, et l'augmentation si nécessaire du nombre de lignes disponibles, sans quoi une exception serait déclenchée pour un index hors limites.
Une autre méthode peut poser problème : il s'agit de celle appliquée lorsque l'utilisateur presse un bouton (btnPushClick). Cette méthode est partagée par tous les boutons de la fenêtre. Afin de déterminer quel bouton a été pressé, on se sert de la propriété TabOrderqui renvoie l'ordre du composant si l'utilisateur utilise la touche de tabulation.
On utilise plutôt la propriété particulière Tagqui a le mérite de ne pas dépendre de l'ordre des composants, mais qui ne vérifie pas qu'elle est unique. Avec TabOrder, on devra revoir le fichier source si l'on modifie l'ordre des composants ou si l'on en ajoute/supprime un. Ici, le choix de TabOrderne se justifie que par le parti pris pédagogique de montrer que plusieurs solutions existent quand il s'agit de résoudre un problème !
En voici la définition :
procedure TMainForm.btnPushClick(Sender: TObject);
// actions
var
LS: string;
begin
case (Sender as TBitBtn).TabOrder of
0 : begin
LS := 'Item : ' + IntToStr(fStackStr.Count);
fStackStr.Push(LS);
end;
1 : LS := 'Pop : ' + fStackStr.Pop;
2 : LS := 'Peek : ' + fStackStr.Peek;
3 : begin
LS := 'Swap';
fStackStr.Swap;
end;
4 : begin
LS := 'Dup';
fStackStr.Dup;
end;
5 : begin
LS := 'Rot';
fStackStr.Rot;
end;
6 : begin
LS := 'Over';
fStackStr.Over;
end;
7 : begin
fStackStr.Clear;
fStackStr.Shrink;
mmoActions.Clear; // on nettoie l'affichage
LS := '*** CLEAR ***';
end;
end;
lblCapacity.Caption := 'Capacité de la pile : ' +
IntToStr(fStackStr.Capacity);
lblDepth.Caption := 'Profondeur de la pile : ' +
IntToStr(fStackStr.Count);
if fStackStr.Error.OK then // si pas d'erreur
MmoActions.Lines.Append(LS) // on affiche
else
fStackStr.Error.Clear; // erreur annulée
end;Une chaîne LSest préparée avant d'être ajoutée au composant TMemo. Comme la taille de la pile peut être modifiée, les composants TLabelcorrespondants sont ajustés.
Il pouvait être plus judicieux de placer cette dernière mise à jour dans la méthode StackChangedqui couvre automatiquement tous les changements de la pile. Le lecteur pourra s'amuser à réaliser ce petit changement. Toutefois, il faut prendre garde de ne pas alourdir démesurément les gestionnaires d'événements qui sont susceptibles d'être appelés de manière très fréquente : on observerait alors un ralentissement général des performances du programme.
IV-B. L'évaluation d'une expression mathématique▲
IV-B-1. Définition▲
Un évaluateur d'expressions mathématiques est un module chargé d'évaluer toute expression qui lui sera soumise, dans la limite des fonctions qu'il connaît.
Le calcul et l'évaluation d'expressions interviennent fréquemment dans les langages de programmation. La notation ordinaire du langage LOGO est la notation dite polonaise : on nomme l'opération pour la faire suivre par ses paramètres. Ainsi la somme de 4 et de 5 s'écrira : SOMME 4 5.
Tant que les calculs sont simples, cette notation ne pose pas de problème, mais elle devient vite difficile à comprendre pour qui utilise d'habitude, comme tout un chacun, la notation infixe : par exemple, SOMME 4 PRODUIT 4 5 donnera comme résultat 4 + (4 x 5), c'est-à -dire 24.
GVLOGO accepte aussi bien la notation polonaise préfixée que la notation infixe utilisée habituellement. Simplement, en cas d'utilisation de cette dernière, l'expression devra être placée entre parenthèses.
L'évaluateur que GVLOGO propose accepte :
- les expressions imbriquées comme (4 * (5,6 / (4 + 8,2)) + 7,1) sans limite particulière d'imbrication ;
- les variables comme :a, :var1, telles que définies par le programme auquel l'évaluation appartient ;
- toute une série de fonctions dont la liste est fournie ci-après ;
- l'interface avec le système de centralisation d'erreurs tel que défini dans l'unité GVErrors ;
- un système de notifications des événements concernant l'état de l'évaluateur.
Les deux systèmes (polonais et notation infixe) ne peuvent pas être utilisés simultanément au sein d'une expression avec parenthèses. On peut donc écrire SOMME 4 (7 * 8), mais pas (4 + PRODUIT 7 8). Une procédure ne peut pas non plus faire partie de l'expression.
GVLOGO utilise la virgule pour les nombres décimaux, conformément à l'usage des écoles. En revanche, comme tous les langages de programmation, il emploie * pour dénoter la multiplication afin d'éviter l'ambiguïté du signe x qui peut être pris pour la lettre.
IV-B-2. Opérations dans l'évaluateur▲
Les fonctions que connaît GVLOGO dans une expression avec parenthèses sont plutôt nombreuses. Elles sont définies dans l'unité GVPrimConsts :
MF_DAbs = 'ABS'; // valeur absolue
MF_DAbs2 = 'ABSOLUE';
MF_DCos = 'COS'; // cosinus
MF_DCos2 = 'COSINUS';
MF_DSin = 'SIN'; // sinus
MF_DSin2 = 'SINUS';
MF_DTan = 'TAN'; // tangente
MF_DTan2 = 'TANGENTE'; // 190
MF_DSqrt = 'RACINE'; // racine carrée
MF_DSqrt2 = 'RAC';
MF_DTrunc = 'TRONQUE'; // nombre tronqué
MF_DRound = 'ARRONDI'; // nombre arrondi
MF_DSqr = 'AU.CARRE'; // nombre au carré
MF_DExp = 'EXP'; // exponentielle
MF_DFrac = 'FRAC'; // partie fractionnelle
MF_DInt = 'ENT'; // partie entière
MF_DInt2 = 'ENTIER';
MF_DLn = 'LN'; // log népérien // 200
MF_DLog2 = 'LOG2'; // log base 2
MF_DLog10 = 'LOG'; // log base 10
MF_DCoTan = 'COTAN'; // cotangente
MF_DCoTan2 = 'COTANGENTE';
MF_DArcCos = 'ARCCOS'; // arc cosinus
MF_DArcCos2 = 'ARCCOSINUS';
MF_DArcSin = 'ARCSIN'; // arc sinus
MF_DArcSin2 = 'ARCSINUS';
MF_DMinus = 'NEGATIF?'; // nombre négatif ?
MF_DPLus = 'POSITIF?'; // nombre positif ? // 210
MF_DNegate = 'OPPOSE'; // signe inversé
MF_DSign = 'SIGNE'; // signe
MF_DRandom = 'HASARD'; // nombre au hasard
MF_Not = 'NON'; // négation
// fonctions sans paramètres
MF_DPi = 'PI'; // PI sur la pile
MF_True = 'VRAI'; // valeur vrai
MF_False = 'FAUX'; // valeur faux
// fonctions infixes
MF_Or = 'OU'; // ou logique
MF_And = 'ET'; // et logique
MF_Mod = 'MOD'; // modulo // 220
MF_DPower = 'PUISSANCE'; // puissanceLes seules fonctions exclues sont celles qui font intervenir deux paramètres sans être infixes : MINIMUM, MAXIMUM…
IV-B-3. Implémentation de l'évaluateur▲
L'implémentation d'un système d'évaluation d'expressions est un problème classique dans le cadre d'une formation en informatique, mais classique ne signifie pas facile. Si des évaluateurs sont disponibles sur Internet, ils sont souvent simplifiés : pas de variables, pas de fonctions, limitation des imbrications… Celui proposé ici tente de lever ces limitations.
IV-B-3-a. Les différentes notations▲
La notation infixe à laquelle nous sommes habitués n'est pas la plus simple à implémenter parce qu'elle doit faire usage de multiples parenthèses pour lever les ambiguïtés et/ou définir de manière claire les priorités des opérations. Par exemple, comment interpréter sans règles l'expression suivante : 4 + 5 * 6 ? Doit-on suivre l'ordre des opérateurs (ce qui donnera 4 + 5 = 9 ; 9 * 6 = 54) ? Dans la pratique, la plupart des langages de programmation fourniront un résultat très différent : 34 (obtenu en faisant 4 + 30 = 34). Ils auront en effet défini une priorité à la multiplication sur l'addition.
Dans le doute ou lorsqu'il veut rendre son travail parfaitement clair, un programmeur fera usage des parenthèses qui sont toujours prioritaires sur les règles de… priorité !
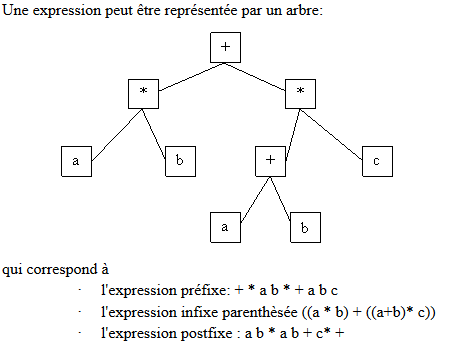
La notation induit alors une lecture particulière de l'arbre, de la racine aux feuilles (notation préfixée ou polonaise, celle native de LOGO) ou au contraire en partant des feuilles pour aller vers la racine (notation postfixée ou polonaise inversée comme dans Forth et certaines calculatrices), ou encore un parcours qui monte et descend dans l'arbre (notation infixe utilisée en général).
Dérivé de LISP, LOGO utilise la notation préfixée, car c'est la plus proche de l'expression naturelle des opérations à effectuer : faire la somme du produit de a et de b, et du produit de la somme de a et de b par c... Si cette « clarté » ne vous paraît pas évidente, essayez d'exprimer les mêmes calculs avec les autres notations…
Le premier intérêt des notations préfixée et postfixée est qu'elles peuvent se passer de parenthèses si le nombre de paramètres de chaque fonction est connu et fixe. Le second intérêt est qu'elles se prêtent très facilement à un traitement par piles, comme celles qui ont été définies dans le chapitre précédent !
On trouve ainsi de nombreuses implémentations d'évaluateurs qui font appel aux structures d'arbres et de piles. Parmi les plus pédagogiques, on consultera avec profit l'article de John Colibri (en français)(21).
IV-B-3-b. L'algorithme shunting-yard (gare de triage)▲
La documentation en français sur cet algorithme est rare alors qu'il est intéressant à plus d'un égard. Voici ce qu'en dit l'article de Wikipédia en anglais :
In computer science, the shunting-yard algorithm is a method for parsing mathematical expressions specified in infix notation. It can be used to produce output in Reverse Polish notation (RPN)
[…]
Like the evaluation of RPN, the shunting yard algorithm is stack-based(22)
Pour ceux qui ne lisent pas l'anglais, disons que cet algorithme convient tout à fait à notre objectif : fondé sur l'utilisation des piles, l'algorithme part d'une expression infixe pour aboutir à une expression postfixée inversée. Il est par ailleurs très rapide, ne faisant appel qu'une seule fois à l'empilement de chaque donnée.
L'algorithme lui-même est complexe : afin de ne pas alourdir le document présent, le renvoi à l'article de Wikipédia suffira. Il faut analyser le texte pour en extraire les unités lexicales de base, les passer à la moulinette de notre algorithme qui utilisera une pile et récupérer la valeur de retour. L'ensemble est légèrement compliqué par une gestion des erreurs.
L'algorithme exige tout d'abord de découper le texte d'entrée en unités de base. On définit par conséquent les différentes catégories possibles de ces unités :
// *** éléments d'une expression à évaluer ***
CTokensEnum = (cteInteger, cteReal, cteVar, cteFunction, cteBeginExp,
cteEndExp, ctePlus, cteMinus, cteMul, cteDiv, ctePower, cteGreater,
cteLower, cteEqual, cteNotEqual, cteGreaterOrEqual, cteLowerOrEqual, cteMod,
cteNot, cteAnd, cteOr, cteOrB, cteAndB, cteBoolean, cteUnKnown,
cteForbidden, cteNotSupported, cteUnaryMinus, cteUnaryPlus);
// *** élément de base d'une expression ***
TGVBaseItem = record
Token: string; // élément
Kind: CTokensEnum; // type d'élément
end;Il exige par ailleurs de définir la priorité de chaque élément, ainsi que le type d'associativité qu'il utilise :
// *** priorité des éléments d'une expression ***
// nombre le plus élevé = priorité la moins élevée
// -1 : ne s'applique pas
// 0: (unaires) - +
// 1: non
// 2: * / % mod
// 3: + -
// 4: > < <= >=
// 5: = <> !=
// 6: &
// 7: |
// 8: et
// 9: ou
// 10: ^ puissance
// 11: ( )
CTokenPrecedence: array [CTokensEnum] of Integer = (-1, -1, -1, -1, 11, 11, 3,
3, 2, 2, 10, 4, 4, 5, 5, 4, 4, 2, 1, 8, 9, 7, 6, -1, -1, -1, -1, 0, 0);
// *** associativité des éléments ***
// 1 = droite - 0 = gauche - -1 = ne s'applique pas
CTokenAssociation: array [CTokensEnum] of Integer = (-1, -1, -1, -1, -1, -1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -1, -1, -1, -1, 0, 0);Pour le suivi de l'état de l'évaluateur, on définit une énumération des états possibles :
// *** états de l'évaluateur ***
TGVEvalState = (esWaiting, esTokenizing, esScanning, esComputing,
esNoInit, esOK);IV-B-3-c. La classe TGVEval▲
L'interface de la classe TGVEvalcomprend de nombreuses méthodes en relation avec les fonctions utilisables dans une expression. On ne reproduit ici que les autres méthodes qui implémentent l'algorithme cité ou le mécanisme des états :
protected
// ajoute un élément au tableau des éléments
procedure AddItem(const AItem: string; AKind: CTokensEnum); virtual;
// ajoute un élément à la liste de scan
procedure AddScan(const AItem: TGVBaseItem); virtual;
procedure GetVar; virtual; // traitement des variables
procedure GetFunction; virtual; // traitement des fonctions
procedure GetNumber; virtual; // traitement des nombres
procedure Change; // notification de changement
procedure StateChange; // notification de changement de l'état
procedure Tokenize; // répartition en éléments
procedure DoScan; // on analyse les éléments
procedure DoEvaluate; // on évalue
public
constructor Create; overload; // constructeur simple
// constructeur avec initialisation
constructor Create(const AText: string); overload;
destructor Destroy; override; // destructeur
procedure Clear; // nettoyage
function GetEnumerator: TGVEvalEnumerator; // énumération
procedure Scan; // étudie la chaîne entrée
function Association(AValue: CTokensEnum): Integer; // associativité
function Precedence(AValue: CTokensEnum): Integer; // priorité
property Text: string read fText write SetText; // expression à analyser
property ActualItem: string read fActualItem; // élément en cours
property Res: Double read fResult; // résultat de l'évaluation
// index de départ
property StartIndx: Integer read fStartIndx write SetStartIndx default 1;
property Indx: Integer read fIndx default -1; // index en cours dans la chaîne
property Count: Integer read GetCount; // nombre d'éléments
property ScanCount: Integer read GetScanCount; // nombre d'éléments après scan
property Item[N: Integer]: TGVBaseItem read GetItem; default; // liste des éléments
property ScanItem[N: Integer]: TGVBaseItem read GetScanItem; // liste pour évaluation
// état de l'évaluateur
property State: TGVEvalState read fEvalState write SetState default esNoInit;
// notification d'une erreur
property Error: TGVErrors read fError write fError;
// événement lié à la recherche d'une variable globale
property Kernel: TGVLogoKernel read fKernel write fKernel;
// événement lié à la recherche d'une variable locale
property LocVars: TGVLocVars read fLocVar write fLocVar;
// événement lié à un changement
property OnChange: TNotifyEvent read fOnChange write fOnChange;
// événement lié à un changement
property OnStateChange: TNotifyEvent read fOnStateChange write fOnStateChange;
end;La méthode centrale est Scan, qui prend en charge les différentes étapes conduisant du texte de départ au résultat :
procedure TGVEval.Scan;
// *** analyse de la chaîne entrée ***
begin
if (State = esNoInit) then // erreur si rien à évaluer
begin
// [### Erreur: non initialisation ###]
Error.SetError(CIE_NoInit, CE_GVLOGO);
Exit; // on sort
end;
try
Change; // notification de changement
Tokenize; // répartition en éléments
if Error.OK then // pas d'erreur ?
DoScan; // on analyse
if Error.Ok then // toujours pas d'erreur ?
DoEvaluate; // on évalue
finally
State := esWaiting; // état d'attente
end;
end;Ces étapes sont par conséquent :
- répartition avec la méthode Tokenize;
- analyse avec la méthode DoScan;
- évaluation avec la méthode DoEvaluate.
On interrompt le travail dès la première erreur rencontrée.
Tokenizes'occupe de balayer la chaîne de caractères d'entrée pour isoler chaque unité lexicale en l'associant à un type :
procedure TGVEval.Tokenize;
// *** répartit en éléments ***
var
LCh: Char;
begin
State := esTokenizing; // état mis à jour
WipeItems; // liste interne nettoyée
fIndx := StartIndx; // départ initialisé
// on balaie l'expression tant qu'il n'y a pas d'erreur
while Error.Ok and (fIndx <= Length(Text)) do
begin
LCh := fText[fIndx]; // caractère en cours
case LCh of
CBlank: Inc(fIndx); // on ignore les blancs
'0'..'9': GetNumber; // c'est un nombre
CColon: GetVar; // c'est une variable
CPlus: if (Count = 0) or (Item[Count].Kind = cteBeginExp) then
AddItem(CPlus, cteUnaryPlus) // plus unaire
else
AddItem(CPlus, ctePlus); // addition ou plus unaire
CMinus: if (Count = 0) or (Item[Count].Kind = cteBeginExp) then
AddItem(CMinus, cteUnaryMinus) // moins unaire
else
AddItem(CMinus, cteMinus); // soustraction ou moins unaire
CMul: AddItem(CMul, cteMul); // multiplication
CDiv: AddItem(CDiv, cteDiv); // division
CPower: AddItem(CPower, ctePower); // puissance
CGreater: GetDelimGreater; // plus grand ou >=
CLower: GetDelimLower; // plus petit ou <= ou <>
CEqual: AddItem(CEqual, cteEqual); // égal
CNot: GetDelimNot; // négation ou !=
COrB: AddItem(COrB, cteOrB); // ou logique |
CAndB: AddItem(CAndB, cteAndB); // et logique &
CBeginPar: AddItem(CBeginPar, cteBeginExp); // parenthèse ouvrante
CEndPar: AddItem(CEndPar, cteEndExp); // parenthèse fermante
'a'..'z', 'A'..'Z': GetFunction; // fonction
else
AddItem(LCh, cteUnknown); // enregistre le caractère interdit
// [### Erreur: caractère interdit ###]
Error.SetError(CE_BadChar, Text, fIndx - 1);
end;
end;
end;Les méthodes appelées sont celles auxquelles une tâche particulière est donnée : par exemple, GetFunctionest une des plus complexes.
Une fois ce travail réalisé, DoScans'occupe d'implémenter l'algorithme de shunting-yard. À la sortie, on doit avoir une liste des ordres rangés selon la notation polonaise inversée : en fait, un tableau d'enregistrements de type TGVBaseItem.
Pour cela, la méthode s'appuie sur le travail précédent, en particulier la répartition des unités par types :
procedure TGVEval.DoScan;
// *** analyse des éléments (algorithme shunting-yard) ***
var
Li: Integer;
LBI1, LBI2: TGVBaseItem;
begin
State := esScanning; // état mis à jour
WipeScan; // nettoyage de la sortie
for Li := 1 to Count do // on balaie la liste
begin
LBI1 := Item[Li]; // élément en cours
case LBI1.Kind of // on analyse sa nature
cteReal, cteInteger, cteVar, cteBoolean: // <==== une constante
AddScan(LBI1); // élément pour la sortie
cteFunction: // <===== une fonction
fScanStack.Push(LBI1);
ctePlus, cteMinus, cteMul, cteDiv, ctePower, cteGreater, cteLower,
cteEqual, cteNotEqual, cteGreaterOrEqual, cteLowerOrEqual, cteMod,
cteNot, cteAnd, cteOr, cteOrB, cteAndB, cteUnaryMinus,
cteUnaryPlus: // <==== un opérateur
begin
while (not fScanStack.IsEmpty) // tant que la pile n'est pas vide
and (((Association(LBI1.Kind) = 0) and (Precedence(LBI1.Kind) >=
Precedence(fScanStack.Peek.Kind))) or
((Association(LBI1.Kind) = 1) and (Precedence(LBI1.Kind) <
Precedence(fScanStack.Peek.Kind)))) do
AddScan(fScanStack.Pop); // on stocke le sommet de la pile
fScanStack.Push(LBI1); // on empile le nouvel opérateur
end;
cteBeginExp: // <==== une parenthèse ouvrante
fScanStack.Push(LBI1); // parenthèse ouvrante empilée
cteEndExp: // <==== une parenthèse fermante
begin
// tant que pile non vide et sommet <> (
while (not fScanStack.IsEmpty) and
(fScanStack.Peek.Kind <> cteBeginExp) do
AddScan(fScanStack.Pop); // on stocke le sommet de la pile
// parenthèse ouvrante trouvée ?
if (not fScanStack.IsEmpty) and
(fScanStack.Peek.Kind = cteBeginExp) then
begin
fScanStack.Pop; // on retire la parenthèse
if (not fScanStack.IsEmpty) and // pile non vide ?
// et fonction au sommet ?
(fScanStack.Peek.Kind = cteFunction) then
AddScan(fScanStack.Pop); // on stocke le sommet de la pile
end
else
begin
// [### Erreur: parenthèses ###]
Error.SetError(CE_ParMismatch, Text, Li);
Break; // on quitte la boucle
end;
end;
end;
end;
if Error.OK then // pas d'erreur ?
begin
while (not fScanStack.IsEmpty) do
begin
LBI2 := fScanStack.Pop; // on récupère le sommet
if (LBI2.Kind in [cteBeginExp, cteEndExp])then
begin
// [### Erreur: parenthèses ###]
Error.SetError(CE_ParMismatch, Text);
Exit; // on quitte la procédure
end
else
AddScan(LBI2); // on stocke
end;
end;
end;La liste obtenue est alors directement exploitable pour l'évaluation proprement dite. Cet ultime travail est effectué par DoEvaluatequi inclut une sous-procédure DoFunction:
procedure TGVEval.DoEvaluate;
// *** évaluation ***
var
Li: Integer;
LWhich: TGVBaseItem;
procedure DoFunction;
// traite une fonction
var
Lfunc: TGVFunctions;
begin
LFunc := WhichFunction(LWhich.Token); // numéro de fonction
if fDStack.Needed(1) then // il faut un élément sur la pile
begin
case LFunc of // choix de la fonction
C_DAbs, C_DAbs2: DoAbs; // valeur absolue
C_DCos, C_DCos2: DoCos; // cosinus
C_DSin, C_DSin2: DoSin; // sinus
C_DTan, C_DTan2: DoTan; // tangente
C_DSqrt, C_DSqrt2: DoSqrt; // racine carrée
C_DTrunc: DoTrunc; // nombre tronqué
C_DRound: DoRound; // nombre arrondi
C_DSqr: DoSqr; // nombre au carré
C_DExp: DoExp; // exponentielle
C_DFrac: DoFrac; // partie fractionnelle
C_DInt, C_DInt2: DoInt; // partie entière
C_DLn: DoLn; // log népérien
C_DLog2: DoLog2; // log base 2
C_DLog10: DoLog10; // log base 10
C_DCoTan, C_DCoTan2: DoCoTan; // cotangente
C_DArcCos, C_DArcCos2: DoArcCos; // arc cosinus
C_DArcSin, C_DArcSin2: DoArcSin; // arc sinus
C_Minus: DoMinus;// négatif ?
C_Plus: DoPlus; // positif ?
C_DNegate: DoNegate; // signe inversé
C_DSign: DoSign; // signe
C_DRandom: DoRandom; // entier au hasard
end;
end
else
// [### Erreur: pas assez d'arguments ###]
Error.SetError(CE_NoArg, Text, Li);
end;L'objectif de cette sous-procédure est de traiter les fonctions rencontrées en les répartissant grâce à une structure case…of.
DoEvaluaterépartit de même tous les autres éléments en balayant tout simplement le tableau réalisé lors des étapes passées :
begin
State := esComputing; // état mis à jour
fResult := 0; // résultat à zéro
for Li := 1 to ScanCount do // on balaie les valeurs
begin
if not Error.OK then
Break; // on sort en cas d'erreur
LWhich := ScanItem[Li]; // élément en cours
fActualItem := LWhich.Token; // élément en cours stocké
Change; // notification de changement
with fDStack do
case LWhich.Kind of // répartition suivant la nature de l'élément
cteReal, cteInteger, cteVar,
cteBoolean: DoNumber(LWhich.Token); // nombre empilé
ctePlus: DoAdd; // addition ?
cteMinus: DoSub; // soustraction
cteMul: DoMul; // multiplication
cteDiv: DoDiv; // divivsion
ctePower: DoPower; // puissance
cteGreater: DoGreater; // >
cteLower: DoLower; // <
cteGreaterOrEqual: DoGreaterOrEqual; // >=
cteLowerOrEqual: DoLowerOrEqual; // <=
cteEqual: DoEqual; // =
cteNotEqual: DoNotEqual; // != ou <>
cteMod: DoMod; // mod
cteNot: DoNot; // non
cteOr, cteOrB: DoOr; // ou
cteAnd, cteAndB: DoAnd; // et
cteFunction: DoFunction; // une fonction
cteUnaryMinus: DoUnaryMinus; // moins unaire
cteUnaryPlus: DoUnaryPlus; // plus unaire
end;
end;
// récupération du résultat si disponible
if Error.OK then // pas d'erreur ?
begin
if fDStack.Count = 1 then // un élément attendu pour le résultat
begin
fResult := fDStack.Pop; // c'est celui qui est sur la pile
State := esOk; // résultat trouvé
Change; // notification de changement
end
else
// [### Erreur: des éléments restent ###]
Error.SetError(CE_BadExp, Text);
end;
end;Le travail se fait par l'usage intensif de la pile fDStackde type TGVDoubleStack. Le résultat final, s'il existe, est récupéré au sommet de cette pile.
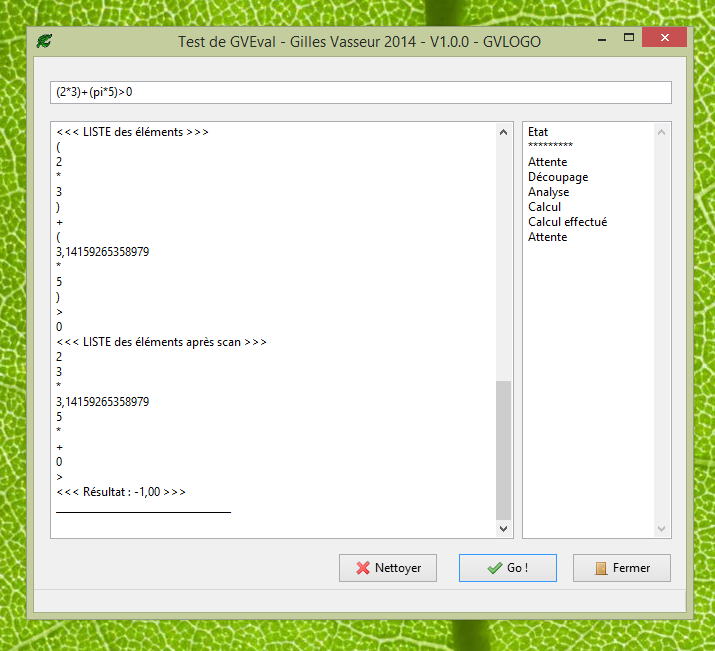
IV-B-3-d. Test de l'unité GVEval▲
Contrairement aux autres unités, l'unité GVEval est fournie avec un programme de test qui ne pourra être compilé qu'après le chapitre suivant. En effet, cette unité est logiquement placée dans la partie « outils de programmation », mais elle fait appel pour l'utilisation des variables au noyau qui sera vu un peu plus tard.
Sans surprise, le programme de test est décliné en deux versions :
- Lazarus pour Windows 32Â ;
- Lazarus pour Linux.
L'intérêt qu'il présente est de rendre explicite chacune des étapes décrites ci-dessus : il affiche aussi bien la décomposition en unités lexicales que la transformation en notation polonaise inversée. Parallèlement sont affichés les différents états de l'évaluateur. Les erreurs provoquent l'interruption de l'évaluation et l'affichage de messages adaptés.
Sans surprise aussi, ce programme de test utilise les éléments déjà vus concernant la gestion des événements :
procedure TMainForm.FormCreate(Sender: TObject);
// création de la fiche
begin
Kernel := TGVLogoKernel.Create; // noyau créé
// on crée des variables
Kernel.AddVar('var1', '123');
Kernel.AddVar('var2', '45,56');
Kernel.AddVar('var3', 'plouf');
Compute := TGVEval.Create; // objet créé
Compute.Kernel := Kernel;
Compute.Error.OnError := @GetError; // gestionnaire d'erreurs
Compute.OnChange := @GetChange; // gestionnaire de changement
Compute.OnStateChange := @GetStateChange; // gestionnaire de changement d'état
end;
