I. Introduction aux interpolations▲
Les programmes de test sont présents dans le répertoire exemples accompagnant le tutoriel.
Free Pascal et Lazarus ne connaissent pas par défaut les fonctions d'interpolation pourtant utiles dès qu'un processus n'est pas linéaire. Le tutoriel qui suit propose une étude des fonctions d'interpolation et une implémentation des courbes d'easing dont disposent d'autres langages. Après la construction de classes dédiées dans un deuxième épisode, une solution alternative à base de courbes de Bézier cubiques viendra clore la série.
I-A. Les interpolations▲
Une interpolation est « une opération mathématique permettant de construire une courbe à partir de la donnée d'un nombre fini de points, ou une fonction à partir de la donnée d'un nombre fini de valeurs ». En ce qui concerne notre sujet d'étude, il faudra prévoir l'évolution d'une fonction pour une durée voulue, depuis un point d'origine et jusqu'à un point d'arrivée. Autrement dit, il s'agira d'appliquer des formules mathématiques personnalisées à des animations : toute valeur évoluant dans le temps pourra être soumise à nos fonctions et classes.
À partir de cet objectif, nous pouvons déjà dégager les données nécessaires à sa réalisation :
- un pas (ou fraction de temps)Â ;
- une durée ;
- une valeur initiale ;
- une valeur finale.
Dans sa forme la plus élémentaire, notre travail produira une interpolation linéaire simple : nous utiliserons une suite arithmétique de raison égale à 1 divisé par le nombre total de pas. Ainsi, pour un début fixé à 0 et une fin fixée à 5, nous aurons une raison de 1/5 (= 0,2) et par conséquent la progression suivante :
|
Valeur de la variable de boucle |
Progression |
|
0 |
0/5 = 0 |
|
1 |
1/5 = 0,2 |
|
2 |
2/5 = 0,4 |
|
3 |
3/5 = 0,6 |
|
4 |
4/5 = 0,8 |
|
5 |
5/5 = 1 |
Si nous prenons comme abscisses les valeurs de la boucle et comme ordonnées les valeurs de progression, nous obtenons un segment de la droite d'équation y = 1/5 x. Un intervalle qui commencerait à la valeur s créerait une droite d'équation y = 1/5 x + s. On ne peut pas imaginer plus simple, plus ordinaire... et plus monotone !
L'idée essentielle du travail à réaliser consiste à soumettre ce déroulement à des fonctions qui ne produisent pas cette suite arithmétique, mais qui aboutissent à la même valeur finale (1 ou 100%).
Par exemple, si nous considérons une interpolation qui calcule des valeurs à partir du carré de la valeur de de la variable de boucle, nous obtenons le tableau suivant :
|
Valeur de la variable de boucle |
Progression |
|
0 |
(0/5)² = 0 |
|
1 |
(1/5)² = 0,04 |
|
2 |
(2/5)² = 0,16 |
|
3 |
(3/5)² = 0,36 |
|
4 |
(4/5)² = 0,64 |
|
5 |
(5/5)² = 1 |
Nous avons bien les mêmes valeurs aux extrémités : 0 et 1. Ces valeurs signifient qu'au bout du compte, que ce soit avec la suite arithmétique ou avec cette formule qui utilise un carré, nous partons du même point d'origine pour arriver au même point final pendant la même durée : seules varient les valeurs intermédiaires.
Qu'apporte ce changement ? À examiner les tableaux, nous nous rendons compte que la progression avec le carré prend du retard sur celle qui est linéaire, mais qu'elle l'a totalement rattrapée à la fin de la boucle.
Voici les courbes représentatives des deux fonctions sur l'intervalle [0 , 1] :
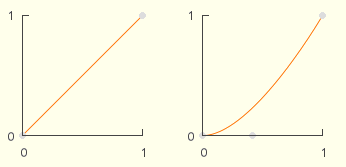
D'un point de vue mathématique, ces résultats s'expliquent facilement : multiplier par lui-même, un nombre positif plus petit que 1 donne un nombre plus petit que le nombre initial ! C'est l'explication du retard. En revanche, ce retard est de moins en moins vrai et disparaît dès que 1 est atteint. L'effet obtenu sera donc celui d'une accélération.
Plus le degré de l'expression sera élevé, plus l'effet sera perceptible : avec des cubes, l'inertie de départ sera encore plus forte, mais le résultat sera au final le même, à savoir 1.
Nous verrons que les degrés ne sont pas les seuls outils à notre disposition : en fait, toute fonction ou combinaison de fonctions qui retourne des valeurs qui partent de 0 pour aboutir à 1 (ou 100%) est une candidate sérieuse à la réalisation d'une interpolation.
Nous pouvons évidemment viser d'autres effets qu'une accélération positive : une décélération est elle aussi tout à fait envisageable.
I-B. Une approche empirique des interpolations▲
[Exemple Interpolations 01]
Pour les besoins du composant TGVTransition qui traite les transitions d'image à image, nous avons déjà donné des éléments pour créer des interpolations. Nous reprenons ci-après les formules empiriques qui ont accompagné ce projet dans sa forme initiale :
function TMainForm.ComputeInterpolation(AStart, AEnd: Integer; AStep: Integer;
AInter: TInterpolation; ABack: Boolean): Integer;
// *** calcul des interpolations ***
function Exponant(AExp: Byte): Integer;
begin
Result := Round((AEnd - AStart) * Power(AStep, AExp) / Power(100, AExp));
end;
function DownExponant(AExp: Byte): Integer;
begin
Result := AEnd - AStart - Round((AEnd - AStart) *
Power(100 - AStep, AExp) / Power(100, AExp));
end;
begin
case AInter of
intLinear: Result := Exponant(1);
intQuadratic: Result := Exponant(2);
intCubic: Result := Exponant(3);
intQuartic: Result := Exponant(4);
intQuintic: Result := Exponant(5);
intSinus: Result := Round(Exponant(1) * sin(pi * AStep / 200));
intSpring: Result := Round(Exponant(1) * (Power(cos(pi * AStep / 100), 2)));
intExpo: Result := Round(Exponant(1) * (Power(2, AStep / 100) - 1));
intSqrt: Result := Round(Exponant(1) * (Sqrt(AStep) / 10));
intSlowDownQuadratic: Result := DownExponant(2);
intSlowDownCubic: Result := DownExponant(3);
intSlowDownQuartic: Result := DownExponant(4);
intSlowDownQuintic: Result := DownExponant(5);
intBounceCos: Result := Exponant(1) + Round((cos(AStep * pi / 100) + 1) * Exponant(1));
intStepsCos: Result := Exponant(1) + Round(Power((cos(AStep * pi / 100) + 1), 2) * 100);
intCos: Result := Round(Exponant(1) * (1 - cos(AStep / 100 * pi)) / 2);
intHalfCos: Result := Round(Exponant(1) * ((1 - cos(AStep /100 * Pi)) / 4 + AStep / 200));
end;
if ABack then
Result := AEnd - Result;
end;L'objectif de la fonction Exponant est de renvoyer une valeur entre AStart et AEnd qui soit modifiée par la puissance utilisée. Par exemple, si la puissance vaut 1, nous obtenons une progression linéaire : en effet, la différence entre AStart et AEnd sera multipliée par le pas à la puissance 1 (elle sera donc inchangée) puis divisée par 100 à la même puissance (donc par 100 inchangé encore une fois). Nous aurons reconnu la formule qui permet de calculer le pourcentage d'une valeur. Pour des puissance supérieures à 1, nous nous retrouvons dans les cas étudiés lors du chapitre précédent.
Comme nous pouvions nous y attendre, la racine carrée ou les puissances de 2 produisent des effets proches des puissances déjà vues. Elles les modulent seulement avec leur propre progression.
Les ralentissements sont obtenus grâce à la fonction imbriquée DownExponant qui inverse les calculs de l'accélération positive par deux soustractions.
Si nous reconnaissons les formules avec des degrés de polynômes, nous découvrons aussi des formules avec des fonctions trigonométriques. Leurs cycles permettent en particulier d'envisager des effets de rebonds.
Pour le moment, contentons-nous d'avoir un aperçu de ce que produisent ces interpolations en action :
Par la suite, il s'agira de formaliser cette approche en la rendant compatible avec celle qu'offrent CSS ou JavaScript par exemple, souvent via des bibliothèques complémentaires.
I-C. Les courbes d'easing▲
Les courbes d'easing qui seront au cœur de ce tutoriel sont des interpolations plus ou moins standardisées que nous retrouvons un peu partout sur Internet dès qu'il est question d'animations.
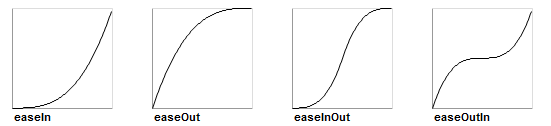
Nous pouvons distinguer des courbes d'easing de quatre types :
- In : l'interpolation suit une formule mathématique d'accélération positive (inertie) ;
- Out : l'interpolation suit une formule d'accélération négative (décélération) ;
- InOut : la première partie de l'interpolation est de type In, la seconde relevant du type Out (inertie, accélération puis décélération);
- OutIn : la première partie est de type Out, la seconde relevant du type In (effet de pause en milieu de parcours avec un premier freinage puis une accélération positive).
De nombreux frameworks ignorent le type OutIn : par exemple, FireMonkey (Delphi) ou .Net. Il peut sembler peu naturel par rapport aux autres, mais nous l'implémenterons malgré tout.
Voici une représentation graphique générale de ces quatre types d'interpolation :
À partir de ces types fondamentaux, les courbes réelles plus ou moins prononcées sont obtenues selon les fonctions, formules ou degrés appliqués.
II. Une application pour le test des courbes d'easing▲
II-A. L'interface de l'application de test▲
[Exemple Interpolations 02]
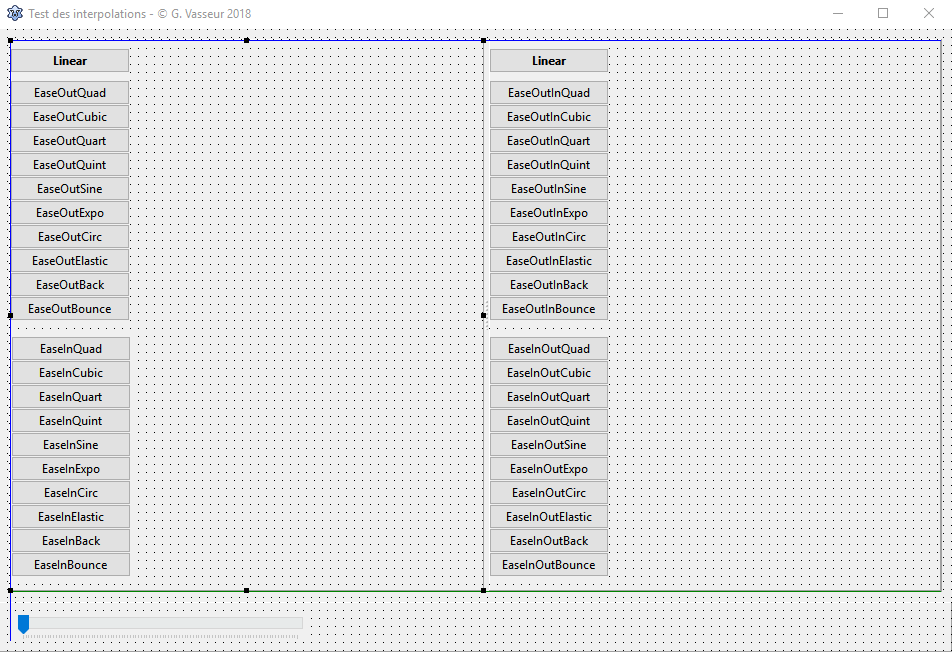
Pour un aperçu efficace des courbes d'easing, nous allons créer une application sans prétention dont l'interface ressemblera à ceci :
Nous reconnaissons :
- trois zones délimitées par des panneaux TPanel (un pour les contrôles de types Out ou In, un pour les contrôles de types InOut ou OutIn et un pour un composant TTrackbar afin d'ajuster la vitesse de l'animation ;
- une séparation ajustable TSplitter entre les deux panneaux supérieurs afin de moduler les distances à parcourir par les contrôles animés (elle est à deviner ;-) ) ;
- des boutons TButton qui serviront d'objets animés (21 dans chaque panneau : 1 pour un repère linéaire et 10 pour chaque type).
Voici le fichier LFM correspondant :
object MainForm: TMainForm
Left = 304
Height = 623
Top = 197
Width = 953
Caption = 'Test des interpolations - © G. Vasseur 2018'
ClientHeight = 623
ClientWidth = 953
OnCreate = FormCreate
LCLVersion = '1.8.2.0'
object pnlMain: TPanel
Left = 10
Height = 553
Top = 10
Width = 933
Align = alClient
BorderSpacing.Around = 10
ClientHeight = 553
ClientWidth = 933
TabOrder = 0
OnClick = btnLinear2Click
object pnlLeft: TPanel
Left = 1
Height = 551
Top = 1
Width = 474
Align = alLeft
ClientHeight = 551
ClientWidth = 474
TabOrder = 0
OnClick = btnLinear2Click
object btnEaseOutBounce: TButton
Left = 0
Height = 25
Top = 256
Width = 120
Caption = 'EaseOutBounce'
OnClick = btnEaseOutQuadClick
TabOrder = 0
end
object btnEaseOutBack: TButton
Left = 0
Height = 25
Top = 232
Width = 120
Caption = 'EaseOutBack'
OnClick = btnEaseOutQuadClick
TabOrder = 1
end
object btnEaseOutElastic: TButton
Left = 0
Height = 25
Top = 208
Width = 120
Caption = 'EaseOutElastic'
OnClick = btnEaseOutQuadClick
TabOrder = 2
end
object btnEaseOutCirc: TButton
Left = 0
Height = 25
Top = 184
Width = 120
Caption = 'EaseOutCirc'
OnClick = btnEaseOutQuadClick
TabOrder = 3
end
object btnEaseOutSine: TButton
Left = 0
Height = 25
Top = 136
Width = 120
Caption = 'EaseOutSine'
OnClick = btnEaseOutQuadClick
TabOrder = 4
end
object btnEaseOutQuint: TButton
Left = 0
Height = 25
Top = 112
Width = 120
Caption = 'EaseOutQuint'
OnClick = btnEaseOutQuadClick
TabOrder = 5
end
object btnEaseOutQuad: TButton
Left = 0
Height = 25
Top = 40
Width = 120
Caption = 'EaseOutQuad'
OnClick = btnEaseOutQuadClick
TabOrder = 6
end
object btnEaseOutCubic: TButton
Left = 0
Height = 25
Top = 64
Width = 120
Caption = 'EaseOutCubic'
OnClick = btnEaseOutQuadClick
TabOrder = 7
end
object btnEaseOutQuart: TButton
Left = 0
Height = 25
Top = 88
Width = 120
Caption = 'EaseOutQuart'
OnClick = btnEaseOutQuadClick
TabOrder = 8
end
object btnEaseOutExpo: TButton
Left = 0
Height = 25
Top = 160
Width = 120
Caption = 'EaseOutExpo'
OnClick = btnEaseOutQuadClick
TabOrder = 9
end
object btnEaseInQuad: TButton
Left = 1
Height = 25
Top = 296
Width = 120
Caption = 'EaseInQuad'
OnClick = btnEaseInQuadClick
TabOrder = 10
end
object btnEaseInCubic: TButton
Left = 1
Height = 25
Top = 320
Width = 120
Caption = 'EaseInCubic'
OnClick = btnEaseInQuadClick
TabOrder = 11
end
object btnEaseInQuart: TButton
Left = 1
Height = 25
Top = 344
Width = 120
Caption = 'EaseInQuart'
OnClick = btnEaseInQuadClick
TabOrder = 12
end
object btnEaseInQuint: TButton
Left = 1
Height = 25
Top = 368
Width = 120
Caption = 'EaseInQuint'
OnClick = btnEaseInQuadClick
TabOrder = 13
end
object btnEaseInSine: TButton
Left = 1
Height = 25
Top = 392
Width = 120
Caption = 'EaseInSine'
OnClick = btnEaseInQuadClick
TabOrder = 14
end
object btnEaseInExpo: TButton
Left = 1
Height = 25
Top = 416
Width = 120
Caption = 'EaseInExpo'
OnClick = btnEaseInQuadClick
TabOrder = 15
end
object btnEaseInCirc: TButton
Left = 1
Height = 25
Top = 440
Width = 120
Caption = 'EaseInCirc'
OnClick = btnEaseInQuadClick
TabOrder = 16
end
object btnEaseInElastic: TButton
Left = 1
Height = 25
Top = 464
Width = 120
Caption = 'EaseInElastic'
OnClick = btnEaseInQuadClick
TabOrder = 17
end
object btnEaseInBack: TButton
Left = 1
Height = 25
Top = 488
Width = 120
Caption = 'EaseInBack'
OnClick = btnEaseInQuadClick
TabOrder = 18
end
object btnEaseInBounce: TButton
Left = 1
Height = 25
Top = 512
Width = 120
Caption = 'EaseInBounce'
OnClick = btnEaseInQuadClick
TabOrder = 19
end
object btnLinear: TButton
Left = 0
Height = 25
Top = 8
Width = 120
Caption = 'Linear'
Font.Style = [fsBold]
OnClick = btnLinear2Click
ParentFont = False
TabOrder = 20
end
end
object pnlRight: TPanel
Left = 480
Height = 551
Top = 1
Width = 452
Align = alClient
ClientHeight = 551
ClientWidth = 452
TabOrder = 1
OnClick = btnLinear2Click
object btnLinear2: TButton
Left = 0
Height = 25
Top = 8
Width = 120
Caption = 'Linear'
Font.Style = [fsBold]
OnClick = btnLinear2Click
ParentFont = False
TabOrder = 0
end
object btnEaseInOutCubic: TButton
Left = 0
Height = 25
Top = 320
Width = 120
Caption = 'EaseInOutCubic'
OnClick = btnEaseInOutQuadClick
TabOrder = 1
end
object btnEaseInOutQuart: TButton
Left = 0
Height = 25
Top = 344
Width = 120
Caption = 'EaseInOutQuart'
OnClick = btnEaseInOutQuadClick
TabOrder = 2
end
object btnEaseOutInQuart: TButton
Left = 0
Height = 25
Top = 88
Width = 120
Caption = 'EaseOutInQuart'
OnClick = btnEaseOutInQuadClick
TabOrder = 3
end
object btnEaseOutInCubic: TButton
Left = 0
Height = 25
Top = 64
Width = 120
Caption = 'EaseOutInCubic'
OnClick = btnEaseOutInQuadClick
TabOrder = 4
end
object btnEaseOutInQuint: TButton
Left = 0
Height = 25
Top = 112
Width = 120
Caption = 'EaseOutInQuint'
OnClick = btnEaseOutInQuadClick
TabOrder = 5
end
object btnEaseInOutQuint: TButton
Left = 0
Height = 25
Top = 368
Width = 120
Caption = 'EaseInOutQuint'
OnClick = btnEaseInOutQuadClick
TabOrder = 6
end
object btnEaseOutInSine: TButton
Left = 0
Height = 25
Top = 136
Width = 120
Caption = 'EaseOutInSine'
OnClick = btnEaseOutInQuadClick
TabOrder = 7
end
object btnEaseInOutQuad: TButton
Left = 0
Height = 25
Top = 296
Width = 120
Caption = 'EaseInOutQuad'
OnClick = btnEaseInOutQuadClick
TabOrder = 8
end
object btnEaseOutInQuad: TButton
Left = 0
Height = 25
Top = 40
Width = 120
Caption = 'EaseOutInQuad'
OnClick = btnEaseOutInQuadClick
TabOrder = 9
end
object btnEaseInOutSine: TButton
Left = 0
Height = 25
Top = 392
Width = 120
Caption = 'EaseInOutSine'
OnClick = btnEaseInOutQuadClick
TabOrder = 10
end
object btnEaseOutInCirc: TButton
Left = 0
Height = 25
Top = 184
Width = 120
Caption = 'EaseOutInCirc'
OnClick = btnEaseOutInQuadClick
TabOrder = 11
end
object btnEaseOutInElastic: TButton
Left = 0
Height = 25
Top = 208
Width = 120
Caption = 'EaseOutInElastic'
OnClick = btnEaseOutInQuadClick
TabOrder = 12
end
object btnEaseOutInBack: TButton
Left = 0
Height = 25
Top = 232
Width = 120
Caption = 'EaseOutInBack'
OnClick = btnEaseOutInQuadClick
TabOrder = 13
end
object btnEaseOutInBounce: TButton
Left = 0
Height = 25
Top = 256
Width = 120
Caption = 'EaseOutInBounce'
OnClick = btnEaseOutInQuadClick
TabOrder = 14
end
object btnEaseOutInExpo: TButton
Left = 0
Height = 25
Top = 160
Width = 120
Caption = 'EaseOutInExpo'
OnClick = btnEaseOutInQuadClick
TabOrder = 15
end
object btnEaseInOutExpo: TButton
Left = 0
Height = 25
Top = 416
Width = 120
Caption = 'EaseInOutExpo'
OnClick = btnEaseInOutQuadClick
TabOrder = 16
end
object btnEaseInOutCirc: TButton
Left = 0
Height = 25
Top = 440
Width = 120
Caption = 'EaseInOutCirc'
OnClick = btnEaseInOutQuadClick
TabOrder = 17
end
object btnEaseInOutElastic: TButton
Left = 0
Height = 25
Top = 464
Width = 120
Caption = 'EaseInOutElastic'
OnClick = btnEaseInOutQuadClick
TabOrder = 18
end
object btnEaseInOutBack: TButton
Left = 0
Height = 25
Top = 488
Width = 120
Caption = 'EaseInOutBack'
OnClick = btnEaseInOutQuadClick
TabOrder = 19
end
object btnEaseInOutBounce: TButton
Left = 0
Height = 25
Top = 512
Width = 120
Caption = 'EaseInOutBounce'
OnClick = btnEaseInOutQuadClick
TabOrder = 20
end
end
object Splitter1: TSplitter
Left = 475
Height = 551
Top = 1
Width = 5
end
end
object pnlBottom: TPanel
Left = 0
Height = 50
Top = 573
Width = 953
Align = alBottom
BorderSpacing.InnerBorder = 10
ClientHeight = 50
ClientWidth = 953
TabOrder = 1
object tbarWait: TTrackBar
Left = 11
Height = 28
Top = 11
Width = 301
Max = 100
OnChange = tbarWaitChange
Position = 0
Align = alLeft
BorderSpacing.Around = 10
TabOrder = 0
end
end
endEn dehors de gestionnaires d'événements sur lesquelles nous reviendrons plus tard, ce fichier révèle les noms des catégories auxquelles seront appliqués les types déjà décrits :
- Quad : application d'une formule du second degré ;
- Cubic : application d'une formule de degré 3 ;
- Quart : application d'une formule de degré 4 ;
- Quint : application d'une formule de degré 5 ;
- Sine : application d'une formule comportant une fonction sinusoïdale ;
- Expo : application d'une formule à base d'exponentielle (puissances de 2) ;
- Circ : application d'une formule à base de cercle ;
- Elastic : formule créant un effet d'élastique à base de fonctions sinusoïdales ;
- Back : formule créant un aller-retour aux extrémités à partir de puissances de 2 et de coefficients particuliers ;
- Bounce : formule créant un effet de rebonds à partir d'une série de sous-formules à base de puissances de 2.
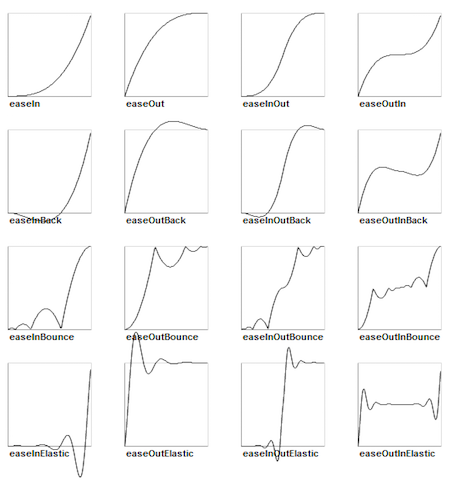
Les courbes dessinées ressembleront à celles-ci :
La première ligne correspond à la catégorie Quad : les autres catégories utilisant des degrés accentuent simplement les effets obtenus.
Toutes ces catégories prendront des paramètres similaires déduits du fonctionnement d'une interpolation. La base est évidemment la formule toute simple de l'interpolation linéaire habituelle :
function TMainForm.EaseNone(AStart, AChange, AStep: Single): Single;
// *** pas de fonction ease ***
begin
Result := AChange * AStep / fDuration + AStart;
end;Nous retrouvons :
- le point de départ : AStart ;
- le point d'arrivée : AChange ;
- le pas (ou intervalle de temps) : AStep ;
- la durée totale de l'interpolation : fDuration.
La formule, encore une fois, ne fait qu'exprimer un pourcentage de réalisation de la valeur finale auquel on aura ajouté la valeur de départ.
Nous avons choisi de traiter à part la durée (d'où son préfixe particulier), car elle est sous contrôle de la valeur du composant de type TTrackbar. Dans cet exemple, nos fonctions n'auront donc que trois paramètres en entrée sur les quatre attendus.
II-B. L'implémentation des fonctions▲
Plusieurs sites proposent les algorithmes permettant de réaliser des fonctions d'easing. Le plus clair à mon avis est celui-ci : ici.
En Pascal, notre ami BeanzMaster propose sa propre implémentation, forcément très proche, mais qui se limite à des fonctions simples, sans les classes que nous développerons plus loin. Vous trouverez ici son travail.
Les paragraphes qui suivent proposent une implémentation originale de ces algorithmes bien connus. Les classes seront construites dans un second temps.
Certains algorithmes font appel à des calculs complexes souvent réduits dans les formules à des valeurs numériques énigmatiques. Ces calculs ne sont pas nécessaires à la compréhension de la suite. Je n'ai parfois trouvé qu'une explication en japonais que les traducteurs automatiques avaient bien du mal à traduire...
II-B-1. Les fonctions utilisant des degrés de polynômes▲
Les fonctions comprenant les termes Quad, Cubic, Quart et Quint s'appuient respectivement sur des formules de degrés 2, 3, 4 et 5.
Elles utilisent les trois méthodes générales suivantes :
function TMainForm.InPower(AStart, AChange, AStep: Single; APower: Integer
): Single;
// *** calcul d'une interpolation de type IN pour les puissances ***
begin
Result := AChange * Power(AStep / fDuration, APower) + AStart;
end;
function TMainForm.OutPower(AStart, AChange, AStep: Single; APower: Integer
): Single;
// *** calcul d'une interpolation de type OUT pour les puissances ***
var
LSign: Integer;
begin
LSign := ifthen(Odd(APower), 1, -1);
Result := LSign * AChange * (Power(AStep / fDuration - 1, APower) + LSign) + AStart;
end;
function TMainForm.InOutPower(AStart, AChange, AStep: Single; APower: Integer
): Single;
// *** calcul d'une interpolation de type INOUT pour les puissances ***
var
LSign: Integer;
begin
LSign := ifthen(Odd(APower), 1, -1);
AStep := AStep / fDuration * 2;
if AStep < 1 then
Result := AChange / 2 * Power(AStep, APower) + AStart
else
Result := LSign * AChange / 2 * (Power(AStep - 2, APower) + LSign * 2) + AStart;
end;Vous pouvez utiliser la fonction ifthen pour simplifier le test des conditions. Cette fonction est présente dans l'unité math qu'il faut donc référencer dans la clause uses de la section implementation de l'unité.
La fonction ifthen prend trois paramètres en entrée :
- une valeur booléenne ;
- une expression renvoyée si la valeur booléenne est vraie ;
- une expression renvoyée si la valeur booléenne est fausse.
Ces fonctions reposent sur l'utilisation de la fonction Power qui renvoie une puissance d'un nombre flottant fourni en paramètre.
Une fois ces bases définies, l'implémentation des fonctions est plutôt simple, voire répétitive !
Voici les fonctions associées à la catégorie Quad (degré 2) :
function TMainForm.EaseInQuad(AStart, AChange, AStep: Single): Single;
// *** INQUAD ***
begin
Result := InPower(AStart, AChange, AStep, 2);
end;
function TMainForm.EaseOutQuad(AStart, AChange, AStep: Single): Single;
// *** OUTQUAD ***
begin
Result := OutPower(AStart, AChange, AStep, 2);
end;
function TMainForm.EaseInOutQuad(AStart, AChange, AStep: Single): Single;
// *** INOUTQUAD ***
begin
Result := InOutPower(AStart, AChange, AStep, 2);
end;
function TMainForm.EaseOutInQuad(AStart, AChange, AStep: Single): Single;
// *** OUTINQUAD ***
begin
if AStep < fDuration / 2 then
Result := EaseOutQuad(AStart, AChange / 2, AStep * 2)
else
Result := EaseInQuad(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;Nous n'avons fait qu'appeler les fonctions de base avec le degré voulu. Il en sera de même pour les fonctions associées à la catégorie Cubic (degré 3) :
function TMainForm.EaseInCubic(AStart, AChange, AStep: Single): Single;
// *** INCUBIC ***
begin
Result := InPower(AStart, AChange, AStep, 3);
end;
function TMainForm.EaseOutCubic(AStart, AChange, AStep: Single): Single;
// *** OUTCUBIC ***
begin
Result := OutPower(AStart, AChange, AStep, 3);
end;
function TMainForm.EaseInOutCubic(AStart, AChange, AStep: Single): Single;
// *** INOUTCUBIC ***
begin
Result := InOutPower(AStart, AChange, AStep, 3);
end;
function TMainForm.EaseOutInCubic(AStart, AChange, AStep: Single): Single;
// *** OUTINCUBIC ***
begin
if AStep < fDuration / 2 then
Result := EaseOutCubic(AStart, AChange / 2, AStep * 2)
else
Result := EaseInCubic(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;Les fonctions relatives à la catégorie Quart (degré 4) ne font pas exception :
function TMainForm.EaseInQuart(AStart, AChange, AStep: Single): Single;
// *** INQUART ***
begin
Result := InPower(AStart, AChange, AStep, 4);
end;
function TMainForm.EaseOutQuart(AStart, AChange, AStep: Single): Single;
// *** OUTQUART ***
begin
Result := OutPower(AStart, AChange, AStep, 4);
end;
function TMainForm.EaseInOutQuart(AStart, AChange, AStep: Single): Single;
// *** INOUTQUART ***
begin
Result := InOutPower(AStart, AChange, AStep, 4);
end;
function TMainForm.EaseOutInQuart(AStart, AChange, AStep: Single): Single;
// *** OUTINQUART ***
begin
if AStep < fDuration / 2 then
Result := EaseOutQuart(AStart, AChange / 2, AStep * 2)
else
Result := EaseInQuart(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;Est-il besoin de préciser qu'il en est de même pour la catégorie Quint (degré 5) ?
function TMainForm.EaseInQuint(AStart, AChange, AStep: Single): Single;
// *** INQUINT ***
begin
Result := InPower(AStart, AChange, AStep, 5);
end;
function TMainForm.EaseOutQuint(AStart, AChange, AStep: Single): Single;
// *** OUTQUINT ***
begin
Result := OutPower(AStart, AChange, AStep, 5);
end;
function TMainForm.EaseInOutQuint(AStart, AChange, AStep: Single): Single;
// *** INOUTQUINT ***
begin
Result := InOutPower(AStart, AChange, AStep, 5);
end;
function TMainForm.EaseOutInQuint(AStart, AChange, AStep: Single): Single;
// *** OUTINQUINT ***
begin
if AStep < fDuration / 2 then
Result := EaseOutQuint(AStart, AChange / 2, AStep * 2)
else
Result := EaseInQuint(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;II-B-2. Les fonctions à base de fonctions sinusoïdales▲
Les fonctions à base de fonctions sinusoïdales font appel, selon le besoin, au sinus ou au cosinus de la valeur en cours à appliquer au point d'arrivée. Le cosinus sera utilisé pour l'accélération positive alors que le sinus conviendra pour la décélération.
Voici les fonctions telles que nous les définirons :
function TMainForm.EaseInSine(AStart, AChange, AStep: Single): Single;
// *** INSINE ***
begin
Result := - AChange * cos(AStep / fDuration * Pi / 2) + AChange + AStart;
end;
function TMainForm.EaseOutSine(AStart, AChange, AStep: Single): Single;
// *** OUTSINE ***
begin
Result := AChange * sin(AStep / fDuration * Pi / 2) + AStart;
end;
function TMainForm.EaseInOutSine(AStart, AChange, AStep: Single): Single;
// *** INOUTSINE ***
begin
Result := - AChange / 2 * (cos(AStep / fDuration * Pi) - 1) + AStart;
end;
function TMainForm.EaseOutInSine(AStart, AChange, AStep: Single): Single;
// *** OUTINSINE ***
begin
if AStep < fDuration / 2 then
Result := EaseOutSine(AStart, AChange / 2, AStep * 2)
else
Result := EaseInSine(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;Finalement, elles ne diffèrent guère des fonctions déjà implémentées : les puissances ont cédé la place aux fonctions trigonométriques, voilà tout ! Nous verrons, à quelques détails près qui tiennent à des valeurs exclues pour certaines fonctions ou à certaines singularités des effets désirés, que notre schéma de départ est applicable la plupart du temps.
II-B-3. Les fonctions exponentielles▲
Sans surprise, la catégorie des fonctions Expo sera implémentée ainsi :
function TMainForm.EaseInExpo(AStart, AChange, AStep: Single): Single;
// *** INEXPO ***
begin
Result := ifthen(AStep = 0, AStart,
AChange * Power(2, 10 * (AStep / fDuration - 1)) + AStart);
end;
function TMainForm.EaseOutExpo(AStart, AChange, AStep: Single): Single;
// *** OUTEXPO ***
begin
Result := ifthen(AStep = fDuration, AChange + AStart,
AChange * (- Power(2, -10 * AStep / fDuration) + 1) + AStart);
end;
function TMainForm.EaseInOutExpo(AStart, AChange, AStep: Single): Single;
// *** INOUTEXPO ***
begin
if AStep = 0 then
Result := AStart
else
if AStep = fDuration then
Result := AChange + AStart
else
begin
AStep := AStep / fDuration * 2;
if AStep < 1 then
Result := AChange / 2 * Power(2, 10 * (AStep - 1)) + AStart
else
Result := AChange / 2 * (- Power(2, - 10 * (AStep - 1)) + 2) + AStart;
end;
end;
function TMainForm.EaseOutInExpo(AStart, AChange, AStep: Single): Single;
// *** OUTINEXPO ***
begin
if AStep < fDuration / 2 then
Result := EaseOutExpo(AStart, AChange / 2, AStep * 2)
else
Result := EaseInExpo(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;II-B-4. Les fonctions fondées sur un cercle▲
Celles relatives au cercle de la catégorie Circ auront l'implémentation suivante :
function TMainForm.EaseInCirc(AStart, AChange, AStep: Single): Single;
// *** INCIRC ***
begin
Result := - AChange * (Sqrt(1 - Power(AStep / fDuration, 2)) - 1) + AStart;
end;
function TMainForm.EaseOutCirc(AStart, AChange, AStep: Single): Single;
// *** OUTCIRC ***
begin
Result := AChange * Sqrt(1 - Power(AStep / fDuration - 1, 2)) + AStart;
end;
function TMainForm.EaseInOutCirc(AStart, AChange, AStep: Single): Single;
// *** INOUTCIRC ***
begin
AStep := AStep / fDuration * 2;
if AStep < 1 then
Result := - AChange / 2 * (Sqrt(1 - Power(AStep, 2)) - 1) + AStart
else
Result := AChange / 2 * (Sqrt(1 - Power(AStep - 2, 2)) + 1) + AStart;
end;
function TMainForm.EaseOutInCirc(AStart, AChange, AStep: Single): Single;
// *** OUTINCIRC ***
begin
if AStep < fDuration / 2 then
Result := EaseOutCirc(AStart, AChange / 2, AStep * 2)
else
Result := EaseInCirc(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;II-B-5. Les fonctions à effet d'élastique▲
Bien sûr, les fonctions de la catégorie Elastic sont plus complexes. Elles s'appuient à la fois sur le caractère amplificateur des puissances de 2 et sur les cycles créés par la fonction sinus :
function TMainForm.EaseInElastic(AStart, AChange, AStep: Single): Single;
// *** INELASTIC ***
begin
if AStep = 0 then
Result := AStart
else
begin
AStep := AStep / fDuration;
if AStep = 1 then
Result := AChange + AStart
else
begin
AStep := AStep - 1;
Result := - (AChange * Power(2, 10 * AStep) * sin((AStep * fDuration
- (fDuration * 0.3 / 4)) * 2 * Pi / (fDuration * 0.3))) + AStart;
end;
end;
end;
function TMainForm.EaseOutElastic(AStart, AChange, AStep: Single): Single;
// *** OUTELASTIC ***
begin
if AStep = 0 then
Result := AStart
else
begin
AStep := AStep / fDuration;
if AStep = 1 then
Result := AChange + AStart
else
Result := AChange * Power(2, - 10 * AStep) * sin((AStep * fDuration -
(fDuration * 0.3 / 4)) * 2 * Pi / (fDuration * 0.3)) + AChange + AStart;
end;
end;
function TMainForm.EaseInOutElastic(AStart, AChange, AStep: Single): Single;
// *** INOUTELASTIC ***
begin
if AStep = 0 then
Result := AStart
else
begin
AStep := AStep / fDuration * 2;
if AStep = 2 then
Result := AChange + AStart
else
begin
// 0.45 = 0.3*1.5 0.1125 = 0.45 / 4
if AStep < 1 then
begin
AStep := AStep - 1;
Result := - (AChange * Power(2, 10 * AStep) * sin((AStep * fDuration -
fDuration * 0.1125) * 2 * Pi / (fDuration * 0.45))) / 2 + AStart;
end
else
begin
AStep := AStep - 1;
Result := AChange * Power(2, - 10 * AStep) * sin((AStep * fDuration -
fDuration * 0.1125) * 2 * Pi / (fDuration * 0.45)) / 2 + AChange + AStart;
end;
end;
end;
end;
function TMainForm.EaseOutInElastic(AStart, AChange, AStep: Single): Single;
// *** OUTINELASTIC ***
begin
if AStep < fDuration / 2 then
Result := EaseOutElastic(AStart, AChange / 2, AStep * 2)
else
Result := EaseInElastic(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;L'effet produit n'en est que plus spectaculaire !
II-B-6. Les fonctions avec aller-retour▲
Les fonctions relatives à la catégorie Back complexifient encore les calculs. Nous les implémenterons en prenant une valeur correspondant à un rebond de 10%, mais d'autres valeurs indiquées dans le code sont utilisables : ces nombres mystérieux cachent en fait des calculs plutôt fastidieux qui permettent de calculer l'amplitude des allers-retours.
Voici l'implémentation adoptée :
function TMainForm.EaseInBack(AStart, AChange, AStep: Single): Single;
// *** INBACK ***
begin
// 1.70158 = 10% 2.592389 = 20% 3.394051 = 30% 4.15574465 = 40%
Result := AChange * Power(AStep / fDuration, 2) * (2.70158 *
AStep / fDuration - 1.70158) + AStart;
end;
function TMainForm.EaseOutBack(AStart, AChange, AStep: Single): Single;
// *** OUTBACK ***
begin
Result := AChange * (Power(AStep / fDuration - 1, 2) *
(2.70158 * (AStep / fDuration - 1) + 1.70158) + 1) + AStart;
end;
function TMainForm.EaseInOutBack(AStart, AChange, AStep: Single): Single;
// *** INOUTBACK ***
begin
// 2.5949095 = 1.70158 * 1.525
AStep := AStep / fDuration * 2;
if AStep < 1 then
Result := AChange / 2 * Power(AStep, 2) * (3.594905 * AStep - 2.594905)
+ AStart
else
Result := AChange / 2 * (Power(AStep - 2, 2) * (3.594905 * (AStep - 2)
+ 2.594905) + 2) + AStart;
end;
function TMainForm.EaseOutInBack(AStart, AChange, AStep: Single): Single;
// *** OUTINBACK ***
begin
if AStep < fDuration / 2 then
Result := EaseOutBack(AStart, AChange / 2, AStep * 2)
else
Result := EaseInBack(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;II-B-7. Les fonctions avec rebonds▲
Enfin, les fonctions relatives à la catégorie Bounce sont les plus longs. Il faut en effet calculer chaque étape afin d'obtenir les résultats les plus proches possibles de rebonds qui paraissent naturels.
Voici l'implémentation adoptée :
function TMainForm.EaseInOutBounce(AStart, AChange, AStep: Single): Single;
// *** INOUTBOUNCE ***
begin
if AStep < fDuration / 2 then
Result := EaseInBounce(0, AChange, AStep * 2) / 2 + AStart
else
Result := EaseOutBounce(0, AChange, AStep * 2 - fDuration) / 2 + AChange / 2
+ AStart;
end;
function TMainForm.EaseOutInBounce(AStart, AChange, AStep: Single): Single;
// *** OUTINBOUNCE ***
begin
if AStep < fDuration / 2 then
Result := EaseOutBounce(AStart, AChange / 2, AStep * 2)
else
Result := EaseInBounce(AStart + AChange / 2, AChange / 2, AStep * 2 - fDuration);
end;
function TMainForm.EaseInBounce(AStart, AChange, AStep: Single): Single;
// *** INBOUNCE ***
begin
Result := AChange - EaseOutBounce(0, AChange, fDuration - AStep) + AStart;
end;
function TMainForm.EaseOutBounce(AStart, AChange, AStep: Single): Single;
// *** OUTBOUNCE ***
begin
AStep := AStep / fDuration;
if AStep < 1 / 2.75 then
Result := AChange * 7.5625 * Power(AStep, 2) + AStart
else
if AStep < 2 / 2.75 then
begin
AStep := AStep - 1.5 / 2.75;
Result := AChange * (7.5625 * Power(AStep, 2) + 0.75) + AStart;
end
else
if AStep < 2.5 / 2.75 then
begin
AStep := AStep - 2.25 / 2.75;
Result := AChange * (7.5625 * Power(AStep, 2) + 0.9375) + AStart;
end
else
begin
AStep := AStep - 2.625 / 2.75;
Result := AChange * (7.5625 * Power(AStep, 2) + 0.984375) + AStart;
end;
end;II-C. L'application de test complète▲
Une fois toutes ces fonctions solidement définies, le reste de l'application ne met en œuvre que des techniques habituelles.
Nous déclarons des constantes pour la valeur de fin à atteindre et la durée par défaut ainsi qu'une énumération afin de différencier les interpolations :
const
C_DefaultDuration = 100;
C_End = 200;
type
TInterpolation = (intLinear,
intEaseInQuad, intEaseOutQuad, intEaseInOutQuad, intEaseOutInQuad,
intEaseInCubic, intEaseOutCubic, intEaseInOutCubic, intEaseOutInCubic,
intEaseInQuart, intEaseOutQuart, intEaseInOutQuart, intEaseOutInQuart,
intEaseInQuint, intEaseOutQuint, intEaseInOutQuint, intEaseOutInQuint,
intEaseInSine, intEaseOutSine, intEaseInOutSine, intEaseOutInSine,
intEaseInExpo, intEaseOutExpo, intEaseInOutExpo, intEaseOutInExpo,
intEaseInCirc, intEaseOutCirc, intEaseInOutCirc, intEaseOutInCirc,
intEaseInElastic, intEaseOutElastic, intEaseInOutElastic, intEaseOutInElastic,
intEaseInBack, intEaseOutBack, intEaseInOutBack, intEaseOutInBack,
intEaseInBounce, intEaseOutBounce, intEaseInOutBounce, intEaseOutInBounce
);Il nous reste à déclarer et définir deux fonctions pour des appels aux fonctions d’interpolation appropriées, l'une renvoyant un nombre flottant, l'autre un entier :
function TMainForm.ComputeInterpolation(AStart, AEnd, AStep: Single;
AInter: TInterpolation; ABack: Boolean): Single;
// *** calcul des interpolations ***
begin
case AInter of
// linéaire
intLinear: Result := EaseNone(AStart, AEnd, AStep);
// quadratique
intEaseInQuad: Result := EaseInQuad(AStart, AEnd, AStep);
intEaseOutQuad: Result := EaseOutQuad(AStart, AEnd, AStep);
intEaseInOutQuad: Result := EaseInOutQuad(AStart, AEnd, AStep);
intEaseOutInQuad: Result := EaseOutInQuad(AStart, AEnd, AStep);
// cubique
intEaseInCubic: Result := EaseInCubic(AStart, AEnd, AStep);
intEaseOutCubic: Result := EaseOutCubic(AStart, AEnd, AStep);
intEaseInOutCubic: Result := EaseInOutCubic(AStart, AEnd, AStep);
intEaseOutInCubic: Result := EaseOutInCubic(AStart, AEnd, AStep);
// quartique
intEaseInQuart: Result := EaseInQuart(AStart, AEnd, AStep);
intEaseOutQuart: Result := EaseOutQuart(AStart, AEnd, AStep);
intEaseInOutQuart: Result := EaseInOutQuart(AStart, AEnd, AStep);
intEaseOutInQuart: Result := EaseOutInQuart(AStart, AEnd, AStep);
// quintique
intEaseInQuint: Result := EaseInQuint(AStart, AEnd, AStep);
intEaseOutQuint: Result := EaseOutQuint(AStart, AEnd, AStep);
intEaseInOutQuint: Result := EaseInOutQuint(AStart, AEnd, AStep);
intEaseOutInQuint: Result := EaseOutInQuint(AStart, AEnd, AStep);
// sinus
intEaseInSine: Result := EaseInSine(AStart, AEnd, AStep);
intEaseOutSine: Result := EaseOutSine(AStart, AEnd, AStep);
intEaseInOutSine: Result := EaseInOutSine(AStart, AEnd, AStep);
intEaseOutInSine: Result := EaseOutInSine(AStart, AEnd, AStep);
// exponentielle
intEaseInExpo: Result := EaseInExpo(AStart, AEnd, AStep);
intEaseOutExpo: Result := EaseOutExpo(AStart, AEnd, AStep);
intEaseInOutExpo: Result := EaseInOutExpo(AStart, AEnd, AStep);
intEaseOutInExpo: Result := EaseOutInExpo(AStart, AEnd, AStep);
// cercle
intEaseInCirc: Result := EaseInCirc(AStart, AEnd, AStep);
intEaseOutCirc: Result := EaseOutCirc(AStart, AEnd, AStep);
intEaseInOutCirc: Result := EaseInOutCirc(AStart, AEnd, AStep);
intEaseOutInCirc: Result := EaseOutInCirc(AStart, AEnd, AStep);
// élastique
intEaseInElastic: Result := EaseInElastic(AStart, AEnd, AStep);
intEaseOutElastic: Result := EaseOutElastic(AStart, AEnd, AStep);
intEaseInOutElastic: Result := EaseInOutElastic(AStart, AEnd, AStep);
intEaseOutInElastic: Result := EaseOutInElastic(AStart, AEnd, AStep);
// retour
intEaseInBack: Result := EaseInBack(AStart, AEnd, AStep);
intEaseOutBack: Result := EaseOutBack(AStart, AEnd, AStep);
intEaseInOutBack: Result := EaseInOutBack(AStart, AEnd, AStep);
intEaseOutInBack: Result := EaseOutInBack(AStart, AEnd, AStep);
// rebond
intEaseInBounce: Result := EaseInBounce(AStart, AEnd, AStep);
intEaseOutBounce: Result := EaseOutBounce(AStart, AEnd, AStep);
intEaseInOutBounce: Result := EaseInOutBounce(AStart, AEnd, AStep);
intEaseOutInBounce: Result := EaseOutInBounce(AStart, AEnd, AStep);
end;
if ABack then
Result := AEnd - Result;
end;
function TMainForm.ComputeInterpolationInt(AStart, AEnd: Integer;
AStep: Integer; AInter: TInterpolation; ABack: Boolean): Integer;
// *** interpolation entière ***
begin
Result := Round(ComputeInterpolation(AStart, AEnd, AStep, AInter, ABack));
end;Comme nous devions l'imaginer, la première fonction n'est qu'une sorte de gare de triage alors que la seconde utilise la première en arrondissant son résultat.
Pour le reste du code, il s'agit de réagir à des clics de souris. Nous permettrons à l'utilisateur de cliquer sur un bouton d'un groupe particulier de manière à ne déclencher les mouvements que pour cet unique groupe, ou sur un des panneaux, ce qui mettra tous les boutons en branle.
Voici le code activé par un clic sur un panneau :
procedure TMainForm.btnLinear2Click(Sender: TObject);
// *** lancement des animations ***
var
Li, LWidth, LWidth2: Integer;
LBack: Boolean;
begin
tbarWait.Enabled := False;
LWidth := pnlLeft.Width - btnLinear2.Width;
LWidth2 := pnlRight.Width - btnLinear.Width;
for LBack := False to True do
for Li := 1 to fDuration do
begin
btnLinear.Left := ComputeInterpolationInt(0, LWidth, Li, intLinear, LBack);
btnLinear2.Left := ComputeInterpolationInt(0, LWidth2, Li, intLinear, LBack);
btnEaseInQuad.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInQuad, LBack);
btnEaseOutQuad.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutQuad, LBack);
btnEaseInOutQuad.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutQuad, LBack);
btnEaseOutInQuad.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInQuad, LBack);
btnEaseInCubic.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInCubic, LBack);
btnEaseOutCubic.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutCubic, LBack);
btnEaseInOutCubic.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutCubic, LBack);
btnEaseOutInCubic.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInCubic, LBack);
btnEaseInQuart.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInQuart, LBack);
btnEaseOutQuart.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutQuart, LBack);
btnEaseInOutQuart.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutQuart, LBack);
btnEaseOutInQuart.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInQuart, LBack);
btnEaseInQuint.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInQuint, LBack);
btnEaseOutQuint.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutQuint, LBack);
btnEaseInOutQuint.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutQuint, LBack);
btnEaseOutInQuint.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInQuint, LBack);
btnEaseInSine.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInSine, LBack);
btnEaseOutSine.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutSine, LBack);
btnEaseInOutSine.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutSine, LBack);
btnEaseOutInSine.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInSine, LBack);
btnEaseInExpo.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInExpo, LBack);
btnEaseOutExpo.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutExpo, LBack);
btnEaseInOutExpo.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutExpo, LBack);
btnEaseOutInExpo.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInExpo, LBack);
btnEaseInCirc.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInCirc, LBack);
btnEaseOutCirc.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutCirc, LBack);
btnEaseInOutCirc.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutCirc, LBack);
btnEaseOutInCirc.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInCirc, LBack);
btnEaseInElastic.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInElastic, LBack);
btnEaseOutElastic.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutElastic, LBack);
btnEaseInOutElastic.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutElastic, LBack);
btnEaseOutInElastic.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInElastic, LBack);
btnEaseInBack.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInBack, LBack);
btnEaseOutBack.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutBack, LBack);
btnEaseInOutBack.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutBack, LBack);
btnEaseOutInBack.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInBack, LBack);
btnEaseInBounce.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInBounce, LBack);
btnEaseOutBounce.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseOutBounce, LBack);
btnEaseInOutBounce.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseInOutBounce, LBack);
btnEaseOutInBounce.Left := ComputeInterpolationInt(0, LWidth2, Li, intEaseOutInBounce, LBack);
sleep(10);
Repaint;
Application.ProcessMessages;
end;
tbarWait.Enabled := True;
end;Les fonctions In seront activées avec :
procedure TMainForm.btnEaseInQuadClick(Sender: TObject);
// *** fonctions IN ***
var
Li, LWidth: Integer;
LBack: Boolean;
begin
tbarWait.Enabled := False;
LWidth := pnlLeft.Width - btnLinear2.Width;
for LBack := False to True do
for Li := 1 to fDuration do
begin
btnLinear.Left := ComputeInterpolationInt(0, LWidth, Li, intLinear, LBack);
btnEaseInQuad.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInQuad, LBack);
btnEaseInCubic.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInCubic, LBack);
btnEaseInQuart.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInQuart, LBack);
btnEaseInQuint.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInQuint, LBack);
btnEaseInSine.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInSine, LBack);
btnEaseInExpo.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInExpo, LBack);
btnEaseInCirc.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInCirc, LBack);
btnEaseInElastic.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInElastic, LBack);
btnEaseInBack.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInBack, LBack);
btnEaseInBounce.Left := ComputeInterpolationInt(0, LWidth, Li, intEaseInBounce, LBack);
sleep(10);
pnlLeft.Repaint;
Application.ProcessMessages;
end;
tbarWait.Enabled := True;
end;Nous renvoyons au code fourni avec le tutoriel pour les autres types de fonction : le code est évidemment similaire.
Reste à gérer la durée qui est une propriété nommée Duration qui elle-même fait référence à un champ privé fDuration à travers un setter :
property Duration: Cardinal read fDuration write SetDuration default C_DefaultDuration;Les méthodes associées sont simples et en relation avec le composant TTrackbar qui fournit la valeur brute de la durée:
procedure TMainForm.tbarWaitChange(Sender: TObject);
// *** changement de la vitesse ***
begin
Duration := tbarWait.Position;
end;
procedure TMainForm.SetDuration(AValue: Cardinal);
// *** détermination de la durée d'interpolation ***
begin
if fDuration = C_End - AValue then
Exit;
fDuration := C_End - AValue;
end;Il ne reste que la création de la fiche à compléter pour obtenir une application fonctionnelle :
procedure TMainForm.FormCreate(Sender: TObject);
// *** création de la fiche ***
begin
Duration := C_DefaultDuration;
tbarWait.Max := C_End;
tbarWait.Position := fDuration;
end;Nous devons en effet renseigner la valeur de la durée par défaut et ajuster correctement les propriétés du composant TTrackbar.
Aucune action n'est nécessaire pour le TSplitter qui saura dimensionner les panneaux suivant le choix de l'utilisateur final.
Voici une vidéo qui montre notre application en action :
III. Conclusion▲
Vous voici parvenus au bout de votre première exploration des interpolations, et plus spécifiquement des courbes d'easing. L'épisode suivant va formaliser ce travail préparatoire en proposant une série de classes à réutiliser dans vos projets à venir.
Mes remerciements vont à Alcatîz et à BeanzMaster pour leur relecture technique et à xxx pour la correction orthographique.